Simplex

Simplex[{p1,…,pk}]

点 piでスパンした単体を表す．

詳細とオプション

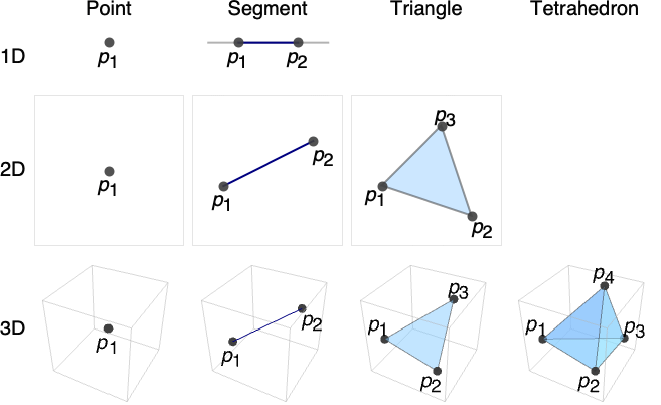
  • Simplexは，点，線分，三角形，四面体，五胞体，hexateron等としても知られている．
  • Simplexは，与えられた点 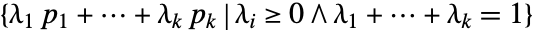の全凸面の組合せを表す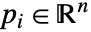．がアフィン独立で 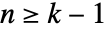のとき．領域は 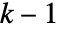次元である．
  • 単体の例．行が埋込み次元に相当する．
  • 整数 n についてのSimplex[n]は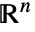，における単位標準単体であるSimplex[{{0,…,0},{1,0,…,0},…,{0,…,0,1}}]に等しい．
  • Simplexは，幾何学領域として，またグラフィックスプリミティブとして使うことができる．
  • グラフィックスでは，点 piはScaled式あるいはDynamic式でよい．
  • グラフィックスの描画はFaceForm，EdgeForm，Opacity，色等の指示子の影響を受ける．

例題

すべて開くすべて閉じる

例  (3)

3DのSimplex：

2D：

異なるスタイルを適用された単体：

体積と重心：

スコープ  (20)

グラフィックス  (9)

指定  (3)

3Dでの標準的な単位Simplex：

3つの点をスパンする2D単体：

次元の単体は，最高で 個の点で指定される：

スタイリング  (3)

異なるスタイルが適用された単体：

色指示子で面の色を指定する：

FaceFormおよびEdgeFormを使って面と辺のスタイルを指定する：

座標  (3)

プロット範囲との割合で座標を指定する：

通常の座標からのスケールされたオフセットを指定する：

点はDynamicでよい：

領域  (11)

埋込み次元は単体がある空間の次元である：

幾何次元は形それ自体の次元である：

点の帰属判定：

点の帰属条件を得る：

測度と重心：

次元 の標準的な単体の測度はである：

点からの距離：

可視化する：

点からの符号付き距離：

点までの最近点：

これを可視化する：

単体は有界である：

その範囲を求める：

単体上でIntegrateする：

単体上で最適化する：

単体上で方程式を解く：

アプリケーション  (1)

次元 のKuhn単体を定義する：

2DのKuhn単体：

3DのKuhn単体：

次元 の測度はである：

次元 の重心はである：

特性と関係  (8)

TriangulateMeshを使って体積メッシュを単体に分割することができる：

MaxCellMeasure等のオプションを使って単体の数を制御する：

PointはSimplexの特殊ケースである：

LineはSimplexの特殊ケースである：

TriangleはSimplexの特殊ケースである：

TetrahedronはSimplexの特殊ケースである：

Polygonは，次元2におけるSimplexの一般化である：

ImplicitRegionは任意のSimplexを表すことができる：

Simplexはその頂点の凸面組合せの集合である：

おもしろい例題  (1)

単体のランダムな集合：

Wolfram Research (2014), Simplex, Wolfram言語関数， https://reference.wolfram.com/language/ref/Simplex.html.

テキスト

Wolfram Research (2014), Simplex, Wolfram言語関数， https://reference.wolfram.com/language/ref/Simplex.html.

CMS

Wolfram Language. 2014. "Simplex." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Simplex.html.

APA

Wolfram Language. (2014). Simplex. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Simplex.html

BibTeX

@misc{reference.wolfram_2024_simplex, author="Wolfram Research", title="{Simplex}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Simplex.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_simplex, organization={Wolfram Research}, title={Simplex}, year={2014}, url={https://reference.wolfram.com/language/ref/Simplex.html}, note=[Accessed: 21-November-2024 ]}