SphericalAngle

SphericalAngle[{θ0,ϕ0}{{θ1,ϕ1},{θ2,ϕ2}}]

gives the signed angle in radians between the great circles through point {θ0,ϕ0} and points {θ1,ϕ1} and {θ2,ϕ2}.

SphericalAngle[p{q,r}]

gives the unsigned angle for points p, q, r of the form {θ1,θ2,…,θn-1,ϕ} on an n-dimensional hypersphere.

SphericalAngle[p{{q1,r1},…,{qn,rn}}]

gives a list of angles between the great circles from point p through points qi and ri.

SphericalAngle[{p1,…,pn}{{q1,r1},…,{qn,rn}}]

gives a list of angles between the great circles from point pi through points qi and ri.

Details

  • Spherical or hyperspherical coordinate vectors use the same conventions of CoordinateChartData and CoordinateTransformData, but with the leading r coordinate dropped.
  • The angle between great circles is measured in radians, and it does not depend on spherical or hyperspherical radius.
  • The spherical case is orientable, so a signed angle is returned. The hyperspherical case is non-orientable without additional input, so an unsigned angle is returned.
  • The sign convention is positive counterclockwise around the normal passing through point p.
  • Points on a 2D sphere can also be specified using GeoPosition[{lat,lon}] notation, with latitudes and longitudes in degrees.
  • When working with numerical data, SphericalAngle does not accept complex-valued inputs and returns only real-valued outputs.

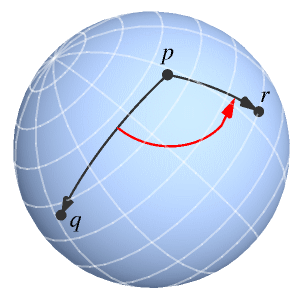
Examples

open allclose all

Basic Examples  (4)

Compute the angle between polar great circles:

Find the angle between a pair of geodesics on the 3-sphere:

Perform a symbolic computation:

Simplify the result assuming a typical range of values:

Calculate 10 random angles on a 4-sphere, all centered around one chosen point:

Scope  (3)

Calculate a symbolic angle between arbitrary points on a sphere:

Calculate the angle around a tetrahedron vertex using 30 digits of precision:

Compare with the exact value:

SphericalAngle also accepts GeoPosition latitude-longitude coordinates:

Applications  (1)

Define three points bounding a spherical octant:

Compute the interior angle at each vertex:

Verify that the sum of these angles minus π equals an eighth of the area of the unit sphere:

Properties & Relations  (3)

GeoDirection computes an angle from the North Pole on an ellipsoidal model of the Earth:

Compute a similar angle on a sphere:

Force GeoDirection to use a spherical model of the Earth:

Approximate the area of the Bermuda Triangle:

Compare with GeoArea, which uses an ellipsoidal model of the Earth:

Take three points on a hypersphere:

The result of SphericalAngle can also be computed using VectorAngle:

Possible Issues  (1)

The angle q-p-r is indeterminate when p and q are antipodal:

Wolfram Research (2024), SphericalAngle, Wolfram Language function, https://reference.wolfram.com/language/ref/SphericalAngle.html.

Text

Wolfram Research (2024), SphericalAngle, Wolfram Language function, https://reference.wolfram.com/language/ref/SphericalAngle.html.

CMS

Wolfram Language. 2024. "SphericalAngle." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SphericalAngle.html.

APA

Wolfram Language. (2024). SphericalAngle. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SphericalAngle.html

BibTeX

@misc{reference.wolfram_2024_sphericalangle, author="Wolfram Research", title="{SphericalAngle}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/SphericalAngle.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_sphericalangle, organization={Wolfram Research}, title={SphericalAngle}, year={2024}, url={https://reference.wolfram.com/language/ref/SphericalAngle.html}, note=[Accessed: 21-December-2024 ]}