StandbyDistribution

StandbyDistribution[dist1,{dist2,…,distn}]

成分の寿命が分布 distiに従う待機分布を表す．成分 i が故障すると成分 i+1がアクティブになる．

StandbyDistribution[dist1,{dist2,…,distn},p]

成分 i から成分 i+1への切換えが確率 p で成功する待機分布を表す．

StandbyDistribution[dist1,{dist2,…,distn},sdist]

交代成分の寿命分布が sdist である待機分布を表す．

StandbyDistribution[dist1,{…,{disti,inactive,disti,active},…},…]

i 番目の成分の寿命分布が，不活発モードでは disti,inactiveに，活発モードの場合は disti,activeに従う待機分布を表す．

詳細

  • StandbyDistribution[…,…]は，成分間の移行が常に成功する完全切換えの系を表す．
  • StandbyDistribution[…,…,s]は，不完全切換えの系を表す．s が分布であるなら，それは切換えの寿命を表す．さもなければ，それは成分間の移行が成功する確率を表す．
  • StandbyDistribution[…,{…,Ai,…},…]は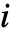，i 番目の成分がアクティブな場合には冷待機分布Aiに従い．アクティブではない場合は悪化しない待機分布を表す．
  • StandbyDistribution[…,{…,{Ii,Ai},…},…]は 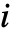i 番目の成分が温待機分布に従う待機分布を表す．成分は，アクティブではない場合は分布 Iiに従ってアクティブな場合は分布 Aiに従って悪化する．
  • 冷待機と温待機の任意の混合からなる成分分布を使うことができる．
  • StandbyDistributionの生存関数およびその他の特性は分布の仮定 dists が{a1A1,a2A2,…,i2I2,i3I3,…,sS,uUniformDistribution[{0,1}]}で与えられる同等のTransformedDistribution[expr,dists]から導出することができる．
  • StandbyDistribution[…]TransformedDistribution[…,dists]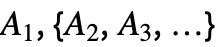
    A_(1),{A_(2),A_(3),...}a1+a2+a3+⋯
    A1,{A2,A3,…},pa1+ a2Boole[p>u]+a3Boole[p2>u]+⋯
    A1,{A2,A3,…},Sa1+a2Boole[s>a1]+a3Boole[s>a1+a2]+⋯
    A1,{{I2,A2},{I3,A3},…}a1+a2Boole[i2>a1]+a3Boole[i3>a1+a2Boole[i2>a1]]+⋯
    A1,{{I2,A2},{I3,A3},…},pa1+a2 Boole[i2>a1∧p>u]+a3Boole[i3>a1+ a2Boole[i2>a1]∧p2>u]+⋯
    A1,{{I2,A2},{I3,A3},…},Sa1+a2 Boole[i2>a1∧s>a1]+a3Boole[i3>a1+a2Boole[i2>a1]∧s>a1+a2Boole[i2>a1]]+⋯
  • StandbyDistributionは，Mean，SurvivalFunction，HazardFunction，ReliabilityDistribution，RandomVariate等の関数で使うことができる．

例題

すべて開くすべて閉じる

例  (3)

完全切換えの冷待機系を定義する：

その確率密度関数を計算する：

故障までの平均時間：

非待機系と比較する：

不完全切換えの冷待機系を定義する：

その確率密度関数を計算する：

故障までの平均時間：

非待機系と比較する：

アクティブではない故障率がアクティブな故障率の半分であるとして，冷待機系と温待機系を定義する：

故障までの平均時間を計算する：

生存関数と比較する：

スコープ  (17)

冷待機と完全切換え  (3)

3つの同一成分で冷待機系を定義する：

故障までの平均時間を計算する：

2つの異なる成分で冷待機系を定義する：

生存関数を計算する：

3つの同一成分が待機している成分を調べる：

確率変量を生成する：

確率密度関数と比較する：

冷待機と不完全切換え  (4)

切換えが確率pで成功する冷待機系：

故障までの平均時間を計算する：

完全切換えと切換えが2回に1回成功する不完全切換えを比較する：

切換えが寿命分布に従ってモデル化されている冷待機系：

生存関数を求める：

より悪い切換えの影響を調べる：

分布に従ってモデル化された3つの成分と1つの切換えの冷待機系：

確率変量を生成する：

確率密度関数と比較する：

成功確率でモデル化された切換え：

確率密度と比較する：

温待機と完全切換え  (3)

成分が待機状態でも故障する待機系：

故障までの平均時間を求める：

待機状態で故障する可能性のある複数の成分を持つ系：

生存関数を冷待機系と比較する：

2つの成分が待機している温待機系：

確率変量を生成する：

確率密度関数と比較する：

温待機と不完全切換え  (4)

切換えが確率pで成功する温待機系：

故障までの平均時間を計算する：

切換えが寿命分布に従う温待機系：

故障までの平均時間を計算する：

切換えが寿命分布に従ってモデル化されている温待機系：

確率変量を生成する：

確率密度関数と比較する：

切換えが確率に従って成功する系：

温待機と冷待機の混合系  (3)

2番目の成分が待機状態で故障することもある待機系：

2番目と3番目の成分の位置が交替する系：

生存関数と比較する：

切換えが確率0.9`で成功する温待機と冷待機の混合系：

ハザード関数を求める：

乱数を生成し確率密度と比較する：

1つの成分が待機状態で故障する可能性を持ち，切換えに寿命がある待機系：

切換えの故障率が異なる生存関数と比較する：

アプリケーション  (2)

ある成分の寿命が指数分布に従っている．信頼性を向上させるために，同じ成分をもう一つ用意した．この2つ目の成分の最も有効な使い方を求める：

一つの方法として並列配置にすることがきる：

あるいは確率pで成功する切換えを使って待機配置にすることもできる：

2つの代替案の生存関数をプロットし，完全切換えを仮定してもとの成分と比較する：

30の待機系について故障回数のシミュレーションを行い，最良の配置を求める：

並列系を使う場合よりも信頼性が高い状態で，切換えをどこまで悪くすることができるかを調べる：

切換えが並列の系と等しくなるための必要条件は，時間とともに低くなることが分かる：

コンピュータサーバについて考える．サーバが所望の機能を持つためには，動力，ハードドライブ，ネットワークカード，ルーターが必要である．動力にはバックアップの電源出力があり，ジーゼル発電機が冷待機している：

ハードドライブはRAID構成で，3つのうち2つが動く必要がある：

ネットワークカードは2番目のカードが待機している：

2つのルーターが並列に接続されている：

結果の生存関数：

これをプロットする：

故障までの平均時間を数値計算する：

このサーバが3ヶ月使える確率を求める：

冗長性が全くない消費者用のバージョンを定義する：

生存関数を比較する：

特性と関係  (9)

冷待機は成分寿命の合計に相当する：

生存関数を比較する：

等しい指数分布に従う成分の冷待機はErlangDistributionである：

成分寿命がExponentialDistributionに従う冷待機はHypoexponentialDistributionに相当する：

StandbyDistributionはTransformedDistributionの特殊ケースである：

生存関数を比較する：

StandbyDistributionはMixtureDistributionの特殊ケースである：

確率密度関数と比較する：

StandbyDistributionはReliabilityDistributionで使うことができる：

生存関数を計算する：

ReliabilityDistributionはStandbyDistributionで使うことができる：

乱数を生成する：

確率密度関数と比較する：

StandbyDistributionはFailureDistributionで使うことができる：

生存関数を計算する：

FailureDistributionはStandbyDistributionで計算することができる：

乱数を生成する：

確率密度関数と比較する：

考えられる問題  (1)

成分分布は正の領域になければならない：

TruncatedDistributionを使って領域が正の値のみになるように制限する：

Wolfram Research (2012), StandbyDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/StandbyDistribution.html.

テキスト

Wolfram Research (2012), StandbyDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/StandbyDistribution.html.

CMS

Wolfram Language. 2012. "StandbyDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/StandbyDistribution.html.

APA

Wolfram Language. (2012). StandbyDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StandbyDistribution.html

BibTeX

@misc{reference.wolfram_2024_standbydistribution, author="Wolfram Research", title="{StandbyDistribution}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/StandbyDistribution.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_standbydistribution, organization={Wolfram Research}, title={StandbyDistribution}, year={2012}, url={https://reference.wolfram.com/language/ref/StandbyDistribution.html}, note=[Accessed: 21-November-2024 ]}