StandbyDistribution
StandbyDistribution[dist1,{dist2,…,distn}]
表示一个具有元件寿命分布为 disti 的备用分布. 当元件 ![]() 失效,元件
失效,元件 ![]() 会激活.
会激活.
StandbyDistribution[dist1,{dist2,…,distn},p]
表示一个成功从元件 ![]() 切换到元件
切换到元件 ![]() 的概率为 p 的备用分布.
的概率为 p 的备用分布.
StandbyDistribution[dist1,{dist2,…,distn},sdist]
表示一个切换元件具有寿命分布 sdist 的备用分布.
StandbyDistribution[dist1,{…,{disti,inactive,disti,active},…},…]
表示第 ![]() 个元件寿命分布在待用模式中遵循 disti,inactive,激活模式中为 disti,active 的备用分布.
个元件寿命分布在待用模式中遵循 disti,inactive,激活模式中为 disti,active 的备用分布.
更多信息

- StandbyDistribution[…,…] 表示一个具有完美切换的系统,其中元件过度总是成功的.
- StandbyDistribution[…,…,s] 表示一个具有不完美切换的系统. 如果 s 是一个分布,它表示切换器的寿命;否则它表示元件间成功过度的概率.
- StandbyDistribution[…,{…,Ai,…},…] 表示第
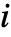 个元件在激活时遵循冷备用分布 Ai,当待用时,不会变质的备用分布.
个元件在激活时遵循冷备用分布 Ai,当待用时,不会变质的备用分布. - StandbyDistribution[…,{…,{Ii,Ai},…},…] 表示第
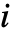 个元件遵循温备用分布的备用分布. 当待用时,元件变质遵循分布 Ii,激活时遵循分布 Ai.
个元件遵循温备用分布的备用分布. 当待用时,元件变质遵循分布 Ii,激活时遵循分布 Ai. - 可以使用任何冷温备用元件分布.
- StandbyDistribution 的生存函数和其他属性可以从具有给定 {a1A1,a2A2,…,i2I2,i3I3,…,sS,uUniformDistribution[{0,1}]} 的分布假设 dists 的等价的 TransformedDistribution[expr,dists] 中导出.
-
StandbyDistribution[…] TransformedDistribution[…,dists] 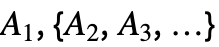
a1+a2+a3+⋯ A1,{A2,A3,…},p a1+ a2Boole[p>u]+a3Boole[p2>u]+⋯ A1,{A2,A3,…},S a1+a2Boole[s>a1]+a3Boole[s>a1+a2]+⋯ A1,{{I2,A2},{I3,A3},…} a1+a2Boole[i2>a1]+a3Boole[i3>a1+a2Boole[i2>a1]]+⋯ A1,{{I2,A2},{I3,A3},…},p a1+a2 Boole[i2>a1∧p>u]+a3Boole[i3>a1+ a2Boole[i2>a1]∧p2>u]+⋯ A1,{{I2,A2},{I3,A3},…},S a1+a2 Boole[i2>a1∧s>a1]+a3Boole[i3>a1+a2Boole[i2>a1]∧s>a1+a2Boole[i2>a1]]+⋯ - StandbyDistribution 可与函数 Mean、SurvivalFunction、HazardFunction、ReliabilityDistribution 和 RandomVariate 一起使用.
范例
打开所有单元关闭所有单元基本范例 (3)
范围 (17)
冷备用和完美切换 (3)
冷备用和不完美切换 (4)
温备用和完美切换 (3)
温备用和不完美切换 (4)
应用 (2)
属性和关系 (9)
具有相同指数分布元件的冷备用是 ErlangDistribution:
冷备用,其中元件寿命遵循对应于 HypoexponentialDistribution 的 ExponentialDistribution:
StandbyDistribution 是 TransformedDistribution 的特殊情形:
StandbyDistribution 是 MixtureDistribution 的特殊情形:
StandbyDistribution 可用于 ReliabilityDistribution:
ReliabilityDistribution 可用于 StandbyDistribution:
StandbyDistribution 可用于 FailureDistribution:
可能存在的问题 (1)
文本
Wolfram Research (2012),StandbyDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/StandbyDistribution.html.
CMS
Wolfram 语言. 2012. "StandbyDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/StandbyDistribution.html.
APA
Wolfram 语言. (2012). StandbyDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/StandbyDistribution.html 年