StateSpaceTransform
StateSpaceTransform[sys,{p,q}]
行列 p および q を使って状態空間モデル sys を変換する.
StateSpaceTransform[sys,{{x1p1[z],…},{z1q1[x],…}}]
変数変換{x1p1[z],…}および{z1q1[x],…}を使って変換する.
詳細とオプション



- StateSpaceTransformは状態変数が変換されている,変換されたモデルを返す.変換は相似変換,同値変換あるいは制約のある同値変換でよい.
- 系 sys は,標準あるいはディスクリプタのStateSpaceModel,AffineStateSpaceModelあるいはNonlinearStateSpaceModelである.
- 標準のStateSpaceModel[{a,b,c,d}]の場合,変換前と変換後の系は変換
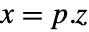 によって関連しており,対応する方程式は以下によって与えられる.
によって関連しており,対応する方程式は以下によって与えられる. -
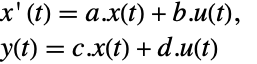
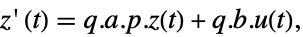
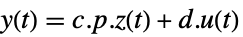
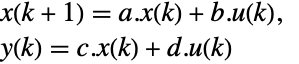
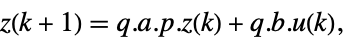
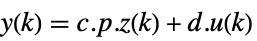
- 一般に,p と q は逆の関係にあり,その場合,変換は相似変換である.p と q の次のデフォルトが標準的なStateSpaceModel変換に使われる.
-
p または {p,Automatic} {p,Inverse[p]} {Automatic,q} {Inverse[q],q} - ディスクリプタStateSpaceModel[{a,b,c,d,e}]については,変換前と変換後の系は変換
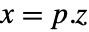 によって関連付けられており,対応する方程式は以下によって与えられる.
によって関連付けられており,対応する方程式は以下によって与えられる. -
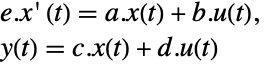
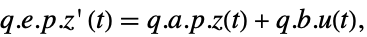
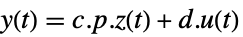
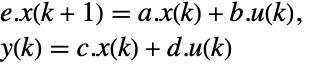
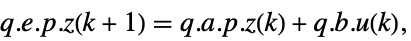
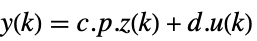
- 一般に,p および q は可逆行列であるが,変換が同値変換になる逆行列ではない.ディスクリプタStateSpaceModel変換には次のデフォルト値が使われる.
-
p または {p,Automatic} {p,IdentityMatrix} {Automatic,q} {IdentityMatrix,q} - ヤコブ行列D[p[z],{z}]の j によるAffineStateSpaceModel[{a,b,c,d},x]およびNonlinearStateSpaceModel[{f,g},x,u]では,変換前の系と変換後の系は変換
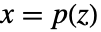 によって関連付けられており,対応する式は以下によって与えらる
によって関連付けられており,対応する式は以下によって与えらる -
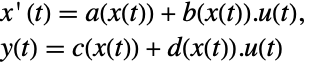
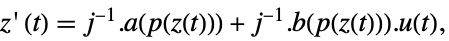
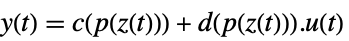
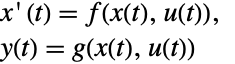
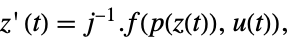
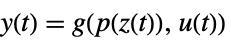
- 一般に,p[z]と q[x]は逆の関係にある.その場合,変換は微分同相写像である.
-
{{x1->p1[z],…},{z1,…}} 必要であれば q[x]が計算される {Automatic,{z1->q[x],…}} p[z]が計算される - 変数変換行列{p,q}が与えられた場合,結果の系は入力と同じタイプである.非線形状態空間モデルの場合,これらは変換規則{{x1->p〚1〛.z,…},{z1->q〚1〛.x,…}}を表すとみなされる.
- 変数変換規則{{x1->p1[z],…},…}が与えられた場合,結果の系は常にAffineStateSpaceModelまたはNonlinearStateSpaceModelである.
- StateSpaceTransformはオプションDescriptorStateSpaceを取る.
例題
すべて開くすべて閉じるスコープ (15)
線形変換 (10)
状態方程式に行列 q を左側から掛けた同値ディスクリプタ系を得る:
ディスクリプタ系では,可逆な p および q を伴う変換は同値系を与える:
非可逆的な p あるいは q は,等価性が制限された系を与える:
線形離散時間系は行列変換では連続時間系と同じような動作をする:
![]() に従ってAffineStateSpaceModelを変換する:
に従ってAffineStateSpaceModelを変換する:
![]() に従ってNonlinearStateSpaceModelを変換する:
に従ってNonlinearStateSpaceModelを変換する:
非線形変換 (5)
オプション (1)
DescriptorStateSpace (1)
アプリケーション (6)
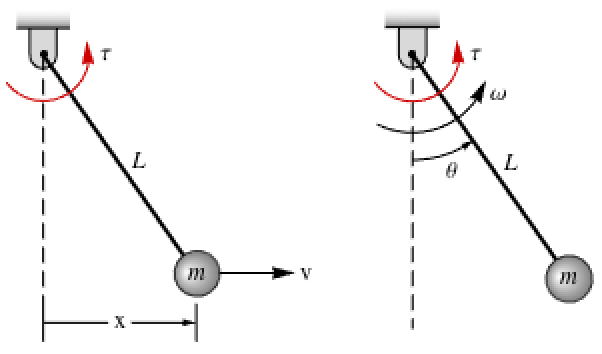
直接球積(dq)変換を,永久磁石ステッピングモーターモデルに適用する:»
特性と関係 (8)
ControllabilityMatrixに基づいたControllableDecomposition:
ObservabilityMatrixに基づいたObservableDecomposition:
ObservabilityGramianに基づいたInternallyBalancedDecomposition:
JordanDecompositionに基づいたJordanModelDecomposition:
座標変換を使った線形化はStateSpaceTransformの使用にも関連している:
テキスト
Wolfram Research (2010), StateSpaceTransform, Wolfram言語関数, https://reference.wolfram.com/language/ref/StateSpaceTransform.html (2014年に更新).
CMS
Wolfram Language. 2010. "StateSpaceTransform." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/StateSpaceTransform.html.
APA
Wolfram Language. (2010). StateSpaceTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StateSpaceTransform.html