StatusCentrality

StatusCentrality[g]

gives a list of status centralities for the vertices in the graph g.

StatusCentrality[{vw,…}]

uses rules vw to specify the graph g.

Details and Options

  • StatusCentrality gives a list of centralities 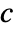that satisfy c=alpha TemplateBox[{a}, Transpose].c+alpha beta, where 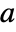is the adjacency matrix of g, 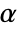is the vector of minimums between the inverse of the largest in- or out-degree of each vertex, and 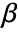is the vertex in-degree of g.
  • The status centrality for an isolated vertex is taken to be zero.
  • StatusCentrality works with undirected graphs, directed graphs, multigraphs, and mixed graphs.

Examples

open allclose all

Basic Examples  (2)

Compute status centralities:

Highlight:

Rank vertices. Highest-ranked vertices are connected from other well-connected vertices:

Scope  (6)

StatusCentrality works with undirected graphs:

Directed graphs:

Multigraphs:

Mixed graphs:

Use rules to specify the graph:

StatusCentrality works with large graphs:

Options  (3)

WorkingPrecision  (3)

By default, StatusCentrality finds centralities using machine-precision computations:

Specify a higher working precision:

Infinite working precision corresponds to exact computation:

Applications  (1)

Highlight the status centrality for StarGraph:

GridGraph:

CompleteKaryTree:

PathGraph:

Properties & Relations  (2)

Status centrality for isolated vertices is taken to be zero:

Use VertexIndex to obtain the centrality of a specific vertex:

Wolfram Research (2012), StatusCentrality, Wolfram Language function, https://reference.wolfram.com/language/ref/StatusCentrality.html (updated 2015).

Text

Wolfram Research (2012), StatusCentrality, Wolfram Language function, https://reference.wolfram.com/language/ref/StatusCentrality.html (updated 2015).

CMS

Wolfram Language. 2012. "StatusCentrality." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/StatusCentrality.html.

APA

Wolfram Language. (2012). StatusCentrality. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StatusCentrality.html

BibTeX

@misc{reference.wolfram_2024_statuscentrality, author="Wolfram Research", title="{StatusCentrality}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/StatusCentrality.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_statuscentrality, organization={Wolfram Research}, title={StatusCentrality}, year={2015}, url={https://reference.wolfram.com/language/ref/StatusCentrality.html}, note=[Accessed: 21-November-2024 ]}