gives a list of authority and hub centralities for the vertices in the graph g.
HITSCentrality[{vw,…}]
uses rules vw to specify the graph g.


HITSCentrality
gives a list of authority and hub centralities for the vertices in the graph g.
HITSCentrality[{vw,…}]
uses rules vw to specify the graph g.
Details and Options
- HITSCentrality is also known as Kleinberg centrality.
- HITSCentrality gives two lists of authority centralities
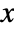 and hub centralities
and hub centralities 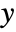 for each vertex.
for each vertex. - If the graph g has adjacency matrix
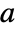 , then authority centralities are given by
, then authority centralities are given by ![TemplateBox[{a}, Transpose].a.x=lambda_1 x TemplateBox[{a}, Transpose].a.x=lambda_1 x](Files/HITSCentrality.en/4.png) , where
, where 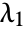 is the largest eigenvalue of
is the largest eigenvalue of ![TemplateBox[{a}, Transpose].a TemplateBox[{a}, Transpose].a](Files/HITSCentrality.en/6.png) , and hub centralities are given by
, and hub centralities are given by 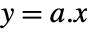 . »
. » - The authority and hub centralities satisfy
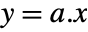 and
and ![x=1/lambda_1TemplateBox[{a}, Transpose].y x=1/lambda_1TemplateBox[{a}, Transpose].y](Files/HITSCentrality.en/9.png) . »
. » - The option WorkingPrecision->p can be used to control the precision used in internal computations.
- HITSCentrality works with undirected graphs, directed graphs, multigraphs, and mixed graphs.
Examples
open all close allBasic Examples (2)
Scope (6)
HITSCentrality works with undirected graphs:
Use rules to specify the graph:
HITSCentrality works with large graphs:
Options (3)
WorkingPrecision (3)
By default, HITSCentrality finds centralities using machine-precision computations:
Specify a higher working precision:
Infinite working precision corresponds to exact computation:
Applications (3)
Highlight the HITS authority and hub centralities for CycleGraph:
A network of web pages linked via hyperlinks. Find the top five informative web pages:
Find the top five pages containing authoritative information:
HITS authority ranking is highly correlated with in-degree ranking:
Find the top five pages containing links to authoritative pages:
HITS hub ranking is highly correlated with out-degree ranking:
Properties & Relations (4)
The authority and hub centrality can be found using the first eigenvector of ![]() :
:
The authority ![]() and hub
and hub ![]() centralities satisfy
centralities satisfy ![]() and
and ![]() :
:
The authority centrality is normalized:
Use VertexIndex to obtain the authority centrality and hub centrality of a specific vertex:
Related Guides
Text
Wolfram Research (2010), HITSCentrality, Wolfram Language function, https://reference.wolfram.com/language/ref/HITSCentrality.html (updated 2015).
CMS
Wolfram Language. 2010. "HITSCentrality." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/HITSCentrality.html.
APA
Wolfram Language. (2010). HITSCentrality. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HITSCentrality.html
BibTeX
@misc{reference.wolfram_2025_hitscentrality, author="Wolfram Research", title="{HITSCentrality}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/HITSCentrality.html}", note=[Accessed: 05-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_hitscentrality, organization={Wolfram Research}, title={HITSCentrality}, year={2015}, url={https://reference.wolfram.com/language/ref/HITSCentrality.html}, note=[Accessed: 05-March-2026]}