gives a list of vertex degrees for the vertices in the underlying simple graph of g.
DegreeCentrality[g,"In"]
gives a list of vertex in-degrees.
DegreeCentrality[g,"Out"]
gives a list of vertex out-degrees.
DegreeCentrality[{vw,…},…]
uses rules vw to specify the graph g.


DegreeCentrality
gives a list of vertex degrees for the vertices in the underlying simple graph of g.
DegreeCentrality[g,"In"]
gives a list of vertex in-degrees.
DegreeCentrality[g,"Out"]
gives a list of vertex out-degrees.
DegreeCentrality[{vw,…},…]
uses rules vw to specify the graph g.
Details
- DegreeCentrality will give high centralities to vertices that have high vertex degrees.
- The vertex degree for a vertex
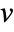 is the number of edges incident to
is the number of edges incident to 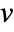 .
. - For a directed graph, the in-degree is the number of incoming edges and the out-degree is the number of outgoing edges.
- For an undirected graph, in-degree and out-degree coincide.
- DegreeCentrality works with undirected graphs, directed graphs, multigraphs, and mixed graphs.
Examples
open all close allBasic Examples (2)
Scope (7)
DegreeCentrality works with undirected graphs:
Use rules to specify the graph:
Compute in-degree and out-degree:
DegreeCentrality works with large graphs:
Applications (8)
Rank vertices by their influence on other vertices in their immediate neighborhood:
Highlight the degree centrality for CycleGraph:
A friendship network in a school. Find the most popular students:
A citation network from the High Energy Physics Phenomenology section of the arXiv e-Print archive. Find the top 10 most-cited articles:
Find the basal species or producers in a food chain:
Find the top species or apex predators:
A network of email sent to the MathGroup list in November 2011. Construct a social network of users, with an edge from ![]() to
to ![]() if
if ![]() has sent at least one reply to
has sent at least one reply to ![]() . Find the users who are the most active at answering questions:
. Find the users who are the most active at answering questions:
Count the users who only received replies and did not send any replies:
Find the users who asked questions most often:
Count the users who only sent replies and did not receive any replies:
The internet at the level of autonomous systems. The frequency of the degree centrality follows a power-law distribution:
Obtain the maximum likelihood parameter estimates, assuming a Zipf distribution:
For graphs with ![]() vertices, the largest sum in differences in degree centrality between the most central vertex and all other vertices is
vertices, the largest sum in differences in degree centrality between the most central vertex and all other vertices is ![]() :
:
Measure how central the most central vertex is with respect to other vertices:
Properties & Relations (5)
The degree of a vertex of an undirected graph is the number of edges incident to the vertex:
For an undirected graph, the in-degree and out-degree centralities coincide:
Use VertexDegree to obtain the degree of a specific vertex:
DegreeCentrality is equivalent to VertexDegree for simple graphs:
For a directed graph, the sum of in- and out-degree centralities is equal to the vertex degree:
Related Guides
Text
Wolfram Research (2010), DegreeCentrality, Wolfram Language function, https://reference.wolfram.com/language/ref/DegreeCentrality.html (updated 2015).
CMS
Wolfram Language. 2010. "DegreeCentrality." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/DegreeCentrality.html.
APA
Wolfram Language. (2010). DegreeCentrality. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DegreeCentrality.html
BibTeX
@misc{reference.wolfram_2025_degreecentrality, author="Wolfram Research", title="{DegreeCentrality}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/DegreeCentrality.html}", note=[Accessed: 23-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_degreecentrality, organization={Wolfram Research}, title={DegreeCentrality}, year={2015}, url={https://reference.wolfram.com/language/ref/DegreeCentrality.html}, note=[Accessed: 23-January-2026]}