KatzCentrality[g,α]
gives a list of Katz centralities for the vertices in the graph g and weight α.
KatzCentrality[g,α,β]
gives a list of Katz centralities using weight α and initial centralities β.
KatzCentrality[{vw,…},…]
uses rules vw to specify the graph g.


KatzCentrality
KatzCentrality[g,α]
gives a list of Katz centralities for the vertices in the graph g and weight α.
KatzCentrality[g,α,β]
gives a list of Katz centralities using weight α and initial centralities β.
KatzCentrality[{vw,…},…]
uses rules vw to specify the graph g.
Details and Options
- KatzCentrality gives a list of centralities
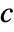 that satisfy
that satisfy ![c=alpha TemplateBox[{a}, Transpose].c+beta c=alpha TemplateBox[{a}, Transpose].c+beta](Files/KatzCentrality.en/2.png) , where
, where 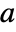 is the adjacency matrix of g.
is the adjacency matrix of g. - If β is a scalar, it is taken to mean {β,β,…}.
- KatzCentrality[g,α] is equivalent to KatzCentrality[g,α,1].
- The option WorkingPrecision->p can be used to control the precision used in internal computations.
- KatzCentrality works with undirected graphs, directed graphs, multigraphs, and mixed graphs.
Examples
open all close allBasic Examples (2)
Scope (8)
KatzCentrality works with undirected graphs:
Use rules to specify the graph:
Nondefault initial centralities:
KatzCentrality works with large graphs:
Options (3)
WorkingPrecision (3)
By default, KatzCentrality finds centralities using machine-precision computations:
Specify a higher working precision:
Infinite working precision corresponds to exact computation:
Applications (6)
Rank vertices of a graph by their importance in their reachable neighborhood:
Highlight the Katz centrality for CycleGraph:
Find the top five most important papers and highlight them:
Predict a partition of the Zachary karate club in case of a conflict between influential members:
Find the most common ancestor in a family tree:
Find descendants at the bottom of the tree:
In a trust network among employees, select employees who could efficiently spread the corporate culture:
Properties & Relations (4)
The centrality vector ![]() satisfies the equation
satisfies the equation ![]() :
:
EigenvectorCentrality is a special case of KatzCentrality:
Take ![]() and
and ![]() with
with ![]() the largest eigenvalue of the adjacency matrix:
the largest eigenvalue of the adjacency matrix:
As ![]() , all vertices get the same centrality:
, all vertices get the same centrality:
Use VertexIndex to obtain the centrality of a specific vertex:
Related Guides
Text
Wolfram Research (2010), KatzCentrality, Wolfram Language function, https://reference.wolfram.com/language/ref/KatzCentrality.html (updated 2015).
CMS
Wolfram Language. 2010. "KatzCentrality." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/KatzCentrality.html.
APA
Wolfram Language. (2010). KatzCentrality. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/KatzCentrality.html
BibTeX
@misc{reference.wolfram_2025_katzcentrality, author="Wolfram Research", title="{KatzCentrality}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/KatzCentrality.html}", note=[Accessed: 25-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_katzcentrality, organization={Wolfram Research}, title={KatzCentrality}, year={2015}, url={https://reference.wolfram.com/language/ref/KatzCentrality.html}, note=[Accessed: 25-January-2026]}