gives a list of eigenvector centralities for the vertices in the graph g.
EigenvectorCentrality[g,"In"]
gives a list of in-centralities for a directed graph g.
EigenvectorCentrality[g,"Out"]
gives a list of out-centralities for a directed graph g.
EigenvectorCentrality[{vw,…},…]
uses rules vw to specify the graph g.


EigenvectorCentrality
gives a list of eigenvector centralities for the vertices in the graph g.
EigenvectorCentrality[g,"In"]
gives a list of in-centralities for a directed graph g.
EigenvectorCentrality[g,"Out"]
gives a list of out-centralities for a directed graph g.
EigenvectorCentrality[{vw,…},…]
uses rules vw to specify the graph g.
Details and Options

- EigenvectorCentrality will give high centralities to vertices that are connected to many other well-connected vertices.
- EigenvectorCentrality gives a list of centralities
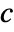 that can be expressed as a weighted sum of centralities of its neighbors.
that can be expressed as a weighted sum of centralities of its neighbors. - With
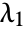 being the largest eigenvalue of the adjacency matrix
being the largest eigenvalue of the adjacency matrix 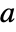 for the graph g, you have:
for the graph g, you have: -
EigenvectorCentrality[g] ![c=TemplateBox[{{{1, /, {lambda, _, 1}}, a}}, Transpose].c c=TemplateBox[{{{1, /, {lambda, _, 1}}, a}}, Transpose].c](Files/EigenvectorCentrality.en/4.png)
EigenvectorCentrality[g,"In"] ![c=TemplateBox[{{{1, /, {lambda, _, 1}}, a}}, Transpose].c c=TemplateBox[{{{1, /, {lambda, _, 1}}, a}}, Transpose].c](Files/EigenvectorCentrality.en/5.png) ,
, 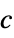 left eigenvector
left eigenvectorEigenvectorCentrality[g,"Out"] 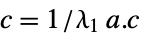 ,
, 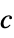 right eigenvector
right eigenvector - Eigenvector centralities are normalized.
- For a directed graph g, EigenvectorCentrality[g] is equivalent to EigenvectorCentrality[g,"In"].
- The option WorkingPrecision->p can be used to control precision used in internal computations.
- EigenvectorCentrality works with undirected graphs, directed graphs, multigraphs, and mixed graphs.
Examples
open all close allBasic Examples (2)
Scope (7)
EigenvectorCentrality works with undirected graphs:
Use rules to specify the graph:
Compute in-centralities and out-centralities:
EigenvectorCentrality works with large graphs:
Options (3)
WorkingPrecision (3)
By default, EigenvectorCentrality finds centralities using machine-precision computations:
Specify a higher working precision:
Infinite working precision corresponds to exact computation:
Applications (9)
Rank vertices by their connectivity to other well-connected vertices:
Order vertices from highest to lowest centrality:
Highlight the eigenvector centrality for CycleGraph:
Find well-connected people in a social network:
Find the most influential members of a student government network with connections from student A to student B, if student A consults student B for opinions:
A citation network from the High Energy Physics Phenomenology section of the arXiv e-Print archive. Find the top 10 important articles:
Find hubs of the internet at the level of autonomous systems:
Hubs are well-connected vertices and have the highest eigenvector centralities:
Find a protein whose deletion will result in lethality in a protein interaction network of yeast:
Protein with the largest eigenvector centrality:
Deleting the protein increases the diameter of the network:
A Saccharomyces cerevisiae protein interaction network. The frequency of the eigenvector centrality follows a power-law distribution:
Obtain the maximum likelihood parameter estimates, assuming a Pareto distribution:
A human-computer system of an organization that deals with internet orders and sends goods by mail. Find departments that should be given the most resources:
Most services rely on a system administration department as well as a register orders department:
Properties & Relations (6)
For undirected graphs, the centrality vector ![]() satisfies the equation
satisfies the equation ![]() :
:
For directed graphs, in-centrality vector ![]() satisfies the equation
satisfies the equation ![]() :
:
Out-centrality vector ![]() satisfies the equation
satisfies the equation ![]() :
:
Eigenvector centralities are normalized:
For disconnected graphs, centralities are normalized with respect to the connected components:
Centrality of the subgraph generated by the connected component:
EigenvectorCentrality is a special case of KatzCentrality:
Use ![]() and
and ![]() as the parameters for KatzCentrality:
as the parameters for KatzCentrality:
Use VertexIndex to obtain the centrality of a specific vertex:
Related Guides
History
Introduced in 2010 (8.0) | Updated in 2012 (9.0) ▪ 2014 (10.0) ▪ 2015 (10.3)
Text
Wolfram Research (2010), EigenvectorCentrality, Wolfram Language function, https://reference.wolfram.com/language/ref/EigenvectorCentrality.html (updated 2015).
CMS
Wolfram Language. 2010. "EigenvectorCentrality." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/EigenvectorCentrality.html.
APA
Wolfram Language. (2010). EigenvectorCentrality. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EigenvectorCentrality.html
BibTeX
@misc{reference.wolfram_2025_eigenvectorcentrality, author="Wolfram Research", title="{EigenvectorCentrality}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/EigenvectorCentrality.html}", note=[Accessed: 03-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_eigenvectorcentrality, organization={Wolfram Research}, title={EigenvectorCentrality}, year={2015}, url={https://reference.wolfram.com/language/ref/EigenvectorCentrality.html}, note=[Accessed: 03-December-2025]}