gives a list of betweenness centralities for the vertices in the graph g.
BetweennessCentrality[{vw,…}]
uses rules vw to specify the graph g.


BetweennessCentrality
gives a list of betweenness centralities for the vertices in the graph g.
BetweennessCentrality[{vw,…}]
uses rules vw to specify the graph g.
Details
- BetweennessCentrality will give high centralities to vertices that are on many shortest paths of other vertex pairs.
- BetweennessCentrality for a vertex
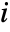 in a connected graph is given by
in a connected graph is given by 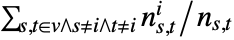 , where
, where 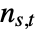 is the number of shortest paths from
is the number of shortest paths from 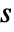 to
to 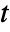 and
and 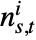 is the number of shortest paths from
is the number of shortest paths from 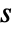 to
to 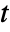 passing through
passing through 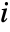 .
. - The ratio
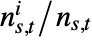 is taken to be zero when there is no path from
is taken to be zero when there is no path from 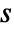 to
to 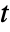 .
. - BetweennessCentrality works with undirected graphs, directed graphs, multigraphs, and mixed graphs.
Examples
open all close allBasic Examples (2)
Scope (6)
BetweennessCentrality works with undirected graphs:
Use rules to specify the graph:
BetweennessCentrality works with large graphs:
Applications (6)
Rank vertices by the fraction of shortest paths between other vertices:
Highlight the betweenness centrality for CycleGraph:
Find the members who can easily withhold or distort information in transmission in a network:
A power grid network representing the topology of the Western States Power Grid of the United States. Identify critical nodes whose failures will most affect the grid:
The neighborhood of the critical nodes:
Find the toll station that would collect the most money in a toll road network:
For graphs with ![]() vertices, the largest sum in differences in betweenness centrality between the most central vertex and all other vertices is
vertices, the largest sum in differences in betweenness centrality between the most central vertex and all other vertices is ![]() :
:
Measure how central the most central vertex is with respect to other vertices:
Properties & Relations (3)
Betweenness centralities for an undirected graph are equivalent to centralities for each component:
Computing the centralities for each component yields the same result:
Betweenness centralities for isolated vertices are taken to be zero:
Use VertexIndex to obtain the centrality of a specific vertex:
Related Guides
Text
Wolfram Research (2010), BetweennessCentrality, Wolfram Language function, https://reference.wolfram.com/language/ref/BetweennessCentrality.html (updated 2015).
CMS
Wolfram Language. 2010. "BetweennessCentrality." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/BetweennessCentrality.html.
APA
Wolfram Language. (2010). BetweennessCentrality. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BetweennessCentrality.html
BibTeX
@misc{reference.wolfram_2025_betweennesscentrality, author="Wolfram Research", title="{BetweennessCentrality}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/BetweennessCentrality.html}", note=[Accessed: 17-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_betweennesscentrality, organization={Wolfram Research}, title={BetweennessCentrality}, year={2015}, url={https://reference.wolfram.com/language/ref/BetweennessCentrality.html}, note=[Accessed: 17-January-2026]}