StraussPointProcess

StraussPointProcess[μ,γ,rs,d]

d内の，一定強度 μ，相互作用パラメータ γ，相互作用半径 rsのStrauss点過程を表す．

詳細

  • StraussPointProcessは点配置を，互いに半径 rs内にあるがそれ以外は一様分布に従っている点を一定の反発対相互作用でモデル化する．
  • Straussモデルは，一般に，過程の相互作用が半径 rs以内の点に対して一定のペナルティを課す，植物の場所，鳥の巣，生体細胞等に使われる．
  •     
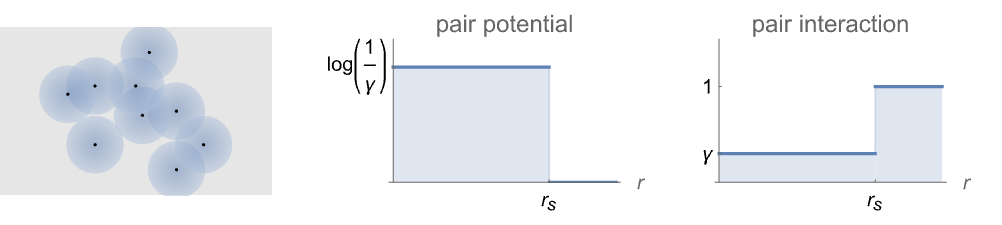
  • Strauss点過程は強度 μ と，どちらも γ と rsによって以下のようにパラメータ化される対ポテンシャル ϕ または対相互作用 h によってGibbsPointProcessとして定義できる．
  • 対ポテンシャル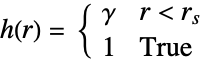
    対相互作用
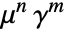  • 観測領域 reg 内のStrauss点過程StraussPointProcess[μ,γ,rs,d]からの点配置は，に比例する密度関数 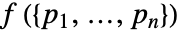を持つ．ただし，PoissonPointProcess[1,d]について m=sum_(i!=j)Boole[TemplateBox[{{{p, _, i}, -, {p, _, j}}}, Norm]<r_s]である．
  • 点 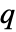を点配置に追加する際のPapangelou条件密度 は である．ただし，m=sum_iBoole[TemplateBox[{{{p, _, i}, -, q}}, Norm]<r_s]である．
  • StraussPointProcessの μ，γ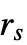，r_(s)は 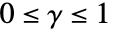である任意の正の数でよく，d は任意の正の整数でよい．
  • StraussPointProcessは 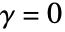のときは簡約されてHardcorePointProcessに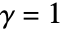，のときはPoissonPointProcessになる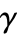．gamma の値が小さい場合は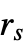，r_(s)よりも点が近くなれない．
  • 次は，RandomPointConfigurationにおけるStraussPointProcessについてのMethodの可能な設定である．
  • "MCMC"マルコフ(Markov)鎖モンテカルロ法による出生死滅過程
    "Exact"過去からのカップリング法
  • 次は，EstimatedPointProcessにおけるStraussPointProcessについてのPointProcessEstimatorの可能な設定である．
  • Automaticパラメータ推定器を自動的に選択する
    "MaximumPseudoLikelihood"擬似尤度を最大にする
  • StraussPointProcessは，RipleyKやRandomPointConfiguration等の関数と一緒に使うことができる．

例題

すべて開くすべて閉じる

例  (2)

Strauss点過程からのサンプル：

サンプル内の点を可視化する：

地理領域からのサンプル：

スコープ  (4)

内のStrauss点過程からのいくつかの実現を生成する：

過程を推定する：

地表のStrauss点過程からのいくつかの実現を生成する：

過程を推定する：

次第に大きくなる相互作用半径でサンプルを生成する：

次第に大きくなる相互作用パラメータ γ でサンプルを生成する：

オプション  (4)

Method  (4)

マルコフ鎖モンテカルロシミュレーション法を使う：

サンプラーへの再帰呼出しの回数を指定する：

実行長を指定する：

シミュレーションに初期状態を与える：

出生死滅過程をさまざまな段階で可視化する：

過去からのカップリングを厳密なサンプリングに使う：

アプリケーション  (1)

Strauss点過程について，単位円板上の点の平均数を計算する：

考えられる問題  (2)

デフォルトで，シミュレーションは点の数が定常状態に収束するまで，あるいはデフォルトの反復回数に達するまで実行される：

サンプラーへの再帰呼出し回数を増やす：

より大きい実行長を指定する：

パラメータ推定のための目的関数は擬似対数尤度関数である：

推定された過程は高い擬似対数尤度を持つ：

どちらの過程も同じようなデータを生成する：

Wolfram Research (2020), StraussPointProcess, Wolfram言語関数， https://reference.wolfram.com/language/ref/StraussPointProcess.html.

テキスト

Wolfram Research (2020), StraussPointProcess, Wolfram言語関数， https://reference.wolfram.com/language/ref/StraussPointProcess.html.

CMS

Wolfram Language. 2020. "StraussPointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/StraussPointProcess.html.

APA

Wolfram Language. (2020). StraussPointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StraussPointProcess.html

BibTeX

@misc{reference.wolfram_2024_strausspointprocess, author="Wolfram Research", title="{StraussPointProcess}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/StraussPointProcess.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_strausspointprocess, organization={Wolfram Research}, title={StraussPointProcess}, year={2020}, url={https://reference.wolfram.com/language/ref/StraussPointProcess.html}, note=[Accessed: 21-November-2024 ]}