-
See Also
- CholeskyDecomposition
- CoreNilpotentDecomposition
- BlockDiagonalMatrix
- BlockLowerTriangularMatrix
- BlockUpperTriangularMatrix
- CauchyMatrix
- DiagonalMatrix
- FourierMatrix
- HadamardMatrix
- HankelMatrix
- HilbertMatrix
- IdentityMatrix
- LowerTriangularize
- LowerTriangularMatrix
- PermutationMatrix
- ToeplitzMatrix
- UpperTriangularize
- UpperTriangularMatrix
- VandermondeMatrix
- Related Guides
-
-
See Also
- CholeskyDecomposition
- CoreNilpotentDecomposition
- BlockDiagonalMatrix
- BlockLowerTriangularMatrix
- BlockUpperTriangularMatrix
- CauchyMatrix
- DiagonalMatrix
- FourierMatrix
- HadamardMatrix
- HankelMatrix
- HilbertMatrix
- IdentityMatrix
- LowerTriangularize
- LowerTriangularMatrix
- PermutationMatrix
- ToeplitzMatrix
- UpperTriangularize
- UpperTriangularMatrix
- VandermondeMatrix
- Related Guides
-
See Also
is an option for linear algebra functions that specifies the representation of the result produced by the function.


TargetStructure
is an option for linear algebra functions that specifies the representation of the result produced by the function.
Details



- An
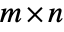 matrix can sometimes be represented with fewer than
matrix can sometimes be represented with fewer than 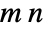 elements, which allows for more efficient storage and more efficient application of operations on the matrix. TargetStructure allows a function to return matrix results in a structured representation, whenever applicable.
elements, which allows for more efficient storage and more efficient application of operations on the matrix. TargetStructure allows a function to return matrix results in a structured representation, whenever applicable. - Possible settings for TargetStructure in functions for constructing matrices include:
-
Automatic automatically choose the representation returned "Dense" represent the matrix as a dense array "Sparse" represent the matrix as a sparse array "Structured" represent the matrix as a structured array - The matrix constructor functions that have the TargetStructure option, and their corresponding supported settings, are as follows:
-
BlockDiagonalMatrix "Dense", "Structured", "Sparse" BlockLowerTriangularMatrix "Dense", "Structured", "Sparse" BlockUpperTriangularMatrix "Dense", "Structured", "Sparse" CauchyMatrix "Dense", "Structured" DiagonalMatrix "Dense", "Structured", "Sparse" FourierMatrix "Dense", "Structured" HankelMatrix "Dense", "Structured" HilbertMatrix "Dense", "Cauchy", "Hankel" IdentityMatrix "Dense", "Structured", "Sparse" LowerTriangularMatrix "Dense", "Structured", "Sparse" PermutationMatrix "Dense", "Structured", "Sparse" ToeplitzMatrix "Dense", "Structured" UpperTriangularMatrix "Dense", "Structured", "Sparse" VandermondeMatrix "Dense", "Structured" - For the functions IdentityMatrix, DiagonalMatrix, ToeplitzMatrix, HankelMatrix and FourierMatrix, the setting TargetStructureAutomatic corresponds to the function returning a dense result below a preset threshold, and a structured array otherwise.
- For all other matrix constructor functions, the setting TargetStructureAutomatic corresponds to returning a structured array result.
- Possible settings for TargetStructure in matrix decomposition functions include:
-
Automatic automatically choose the representation returned "Dense" represent all matrices as dense arrays "Structured" represent all matrices as structured arrays, whenever possible - The matrix decomposition functions that have the TargetStructure option, and their corresponding supported settings, are as follows:
-
CholeskyDecomposition "Dense", "Structured" CoreNilpotentDecomposition "Dense", "Structured" - The functions LowerTriangularize and UpperTriangularize also support the TargetStructure option. Possible settings include:
-
Automatic preserve the type of the input matrix "Dense" represent the matrix as a dense array "Sparse" represent the matrix as a sparse array "Structured" represent the matrix as a structured array - With the setting TargetStructure"Structured", LowerTriangularize returns a LowerTriangularMatrix result, while UpperTriangularize returns an UpperTriangularMatrix result, whenever applicable.
- The setting TargetStructureNone is equivalent to TargetStructure"Dense".
Examples
open all close allBasic Examples (3)
Return the identity matrix as a structured array instead:
Return the identity matrix as a sparse array:
For IdentityMatrix, the setting Automatic determines the structure based on matrix size:
Scope (8)
Matrix Constructors (4)
A rectangular diagonal matrix:
This is equivalent to the explicit setting TargetStructure"Dense":
Return the diagonal matrix as a sparse array:
Return the diagonal matrix as a structured array:
Return a Hankel matrix as a structured array:
Return a Cauchy matrix as a dense matrix:
Matrix Decompositions (2)
Cholesky decomposition of a Hilbert matrix:
Represent the Cholesky triangle as an UpperTriangularMatrix:
Core-nilpotent decomposition of a matrix, with the core and nilpotent parts in a single matrix:
With TargetStructure"Structured", the core and nilpotent parts are brought together in a BlockDiagonalMatrix:
Other Functions (2)
With TargetStructure"Dense", the function UpperTriangularize returns a dense matrix:
With TargetStructure"Sparse", a sparse array is returned:
With TargetStructure"Structured", a structured array is returned:
With the setting TargetStructureAutomatic, the function LowerTriangularize gives a dense matrix if the input is a dense matrix:
If the input is a sparse array, the result is also a sparse array:
Applications (3)
Generate a large identity matrix as a dense matrix:
Computing its determinant takes some time:
Generate the identity matrix as a structured matrix:
Computing the determinant of the structured version is faster:
Generate a Fourier matrix as a dense matrix:
Generate a random complex vector:
This multiplies the Fourier matrix and the vector:
Generate the Fourier matrix as a structured matrix:
Multiplication using the structured version is faster:
Generate a Hilbert matrix as a dense matrix:
Generate a random real vector:
Solve a linear system with the Hilbert matrix:
Generate the Hilbert matrix as a Cauchy matrix:
Solving the linear system using the Cauchy version is faster:
Properties & Relations (4)
The setting TargetStructureAutomatic produces a dense matrix for small dimensions:
A structured array is returned for large dimensions:
The setting TargetStructure"Dense" produces a dense matrix:
The setting TargetStructureNone does the same thing:
The setting TargetStructure"Sparse" produces a sparse array, whenever possible:
The setting TargetStructure"Structured" produces a structured array, whenever possible:
See Also
CholeskyDecomposition CoreNilpotentDecomposition BlockDiagonalMatrix BlockLowerTriangularMatrix BlockUpperTriangularMatrix CauchyMatrix DiagonalMatrix FourierMatrix HadamardMatrix HankelMatrix HilbertMatrix IdentityMatrix LowerTriangularize LowerTriangularMatrix PermutationMatrix ToeplitzMatrix UpperTriangularize UpperTriangularMatrix VandermondeMatrix
Related Guides
History
Text
Wolfram Research (2023), TargetStructure, Wolfram Language function, https://reference.wolfram.com/language/ref/TargetStructure.html.
CMS
Wolfram Language. 2023. "TargetStructure." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TargetStructure.html.
APA
Wolfram Language. (2023). TargetStructure. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TargetStructure.html
BibTeX
@misc{reference.wolfram_2025_targetstructure, author="Wolfram Research", title="{TargetStructure}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/TargetStructure.html}", note=[Accessed: 22-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_targetstructure, organization={Wolfram Research}, title={TargetStructure}, year={2023}, url={https://reference.wolfram.com/language/ref/TargetStructure.html}, note=[Accessed: 22-December-2025]}