CoreNilpotentDecomposition

CoreNilpotentDecomposition[m]

yields the core-nilpotent decomposition of a square matrix m.

CoreNilpotentDecomposition[m,format]

returns the core-nilpotent decomposition according to the specified format.

Details and Options

CoreNilpotentDecomposition[m] returns a list of matrices {t,c,n} where the core matrix c is nonsingular and the matrix n is nilpotent. »
The matrix m is related to its core-nilpotent decomposition by .
For the nilpotent matrix n, there exists a non-negative integer 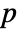(the index of the matrix m) such that MatrixPower[n,p] is the zero matrix.
The core-nilpotent decomposition of a matrix can be used for solving systems of linear differential-algebraic (or difference-algebraic) equations with constant coefficients.
If either the core or nilpotent parts are trivial, an empty list {} is returned for the trivial part. »
CoreNilpotentDecomposition[m] is equivalent to CoreNilpotentDecomposition[m,"SplitBlocks"].
CoreNilpotentDecomposition[m,"BlockDiagonal"] returns a list of matrices {t,d} where .
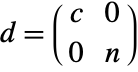With the setting TargetStructure->"Dense", CoreNilpotentDecomposition[m,"BlockDiagonal"] returns a list of matrices {t,d} where .
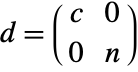With the setting TargetStructure->"Structured", the matrix 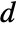in the list {t,d} is represented as a BlockDiagonalMatrix.

Examples

open allclose all

Basic Examples (2)

Compute the core-nilpotent decomposition of a square matrix:

Format the result:

Core-nilpotent decomposition of a 4×4 matrix:

Verify the relation with m:

Scope (12)

Basic Uses (7)

Core-nilpotent decomposition of a machine-precision matrix:

Core-nilpotent decomposition of a complex matrix:

Core-nilpotent decomposition of an exact matrix:

Core-nilpotent decomposition of an arbitrary-precision matrix:

Core-nilpotent decomposition of a symbolic matrix:

The decomposition of large machine-precision matrices is efficient:

CoreNilpotentDecomposition[m] is equivalent to CoreNilpotentDecomposition[m,"SplitBlocks"], where the core and nilpotent parts are kept separate:

CoreNilpotentDecomposition[m,"BlockDiagonal"] brings the core and nilpotent parts together in a block diagonal matrix:

Special Matrices (5)

Core-nilpotent decomposition of a sparse matrix:

Core-nilpotent decomposition of a structured matrix:

The identity matrix has a trivial core-nilpotent decomposition:

Core-nilpotent decomposition of a Hilbert matrix:

Core-nilpotent decomposition of a strictly upper triangular matrix:

Options (1)

TargetStructure (1)

With TargetStructure->"Dense", CoreNilpotentDecomposition[m,"BlockDiagonal"] returns a list of two matrices:

The second matrix is a block diagonal matrix consisting of the core and nilpotent parts:

With TargetStructure->"Structured", the second matrix is represented as a BlockDiagonalMatrix:

Applications (2)

Solve the matrix differential equation , with singular coefficients:

Both and are singular, so the equation cannot be put in the standard form :

Compute the core-nilpotent decomposition of the solution to :

Let :

The solution is then , where is the solution to :

Compare with the result given by DSolveValue:

Find the general solution of the matrix difference equation with singular coefficient matrix :

The matrix is singular:

Using the core-nilpotent decomposition , let :

The solution is , where is an arbitrary vector:

Verify the solution:

Properties & Relations (4)

CoreNilpotentDecomposition returns a triple {t,c,n}:

The matrix c is nonsingular:

The matrix n is nilpotent:

The original matrix m can be expressed in terms of its core-nilpotent decomposition:

The core part of the decomposition for an invertible matrix is equal to the matrix:

The nilpotent part of the decomposition is an empty list:

The similarity matrix t is taken to be the identity matrix:

The identity expressed using BlockDiagonalMatrix holds nonetheless:

The nilpotent part of the decomposition for a nilpotent matrix is equal to the matrix:

The core part of the decomposition is an empty list:

The similarity matrix t is taken to be the identity matrix:

The identity expressed using BlockDiagonalMatrix holds nonetheless:

DrazinInverse can be computed with CoreNilpotentDecomposition:

Verify the equality $m^D=t.(TemplateBox[{c}, Inverse] 0; 0 0).TemplateBox[{t}, Inverse]$ :

Possible Issues (2)

The core-nilpotent decomposition is not unique:

Either or , but not both, can be equal to {}:

MatrixQ[{}] gives False:

Use BlockDiagonalMatrix to reconstruct the original matrix, since it interprets {} as a 0×0 matrix:

Top

CoreNilpotentDecomposition

Details and Options

Examples

Basic Examples (2)