WOLFRAM

Wolfram 语言与系统 参考资料中心
Wolfram 语言首页 »

TensorSymmetry
✖
TensorSymmetry

✖
TensorSymmetry[tensor]

在位置的置换下，给出 tensor 的对称性.

✖
TensorSymmetry[tensor,slots]

在指定位置列表的置换下，给出对称性.

更多信息和选项

  • TensorSymmetry 接受任意类型的张量，或者是符号式或者是显式，包括任意类型的数组.
  • 普通对称性由 {perm,ϕ} 对的生成集合指定，其中 perm 是张量位置的排列，而 ϕ 是单位根. 每一对表示形式为 ϕ TensorTranspose[tensor,perm]==tensor 的张量的对称性.
  • 某些对称指定具有名称：
  • Symmetric[{s1,…,sn}]位置 si 中的完全对称性
    Antisymmetric[{s1,…,sn}]位置 si 中的反对称性
    ZeroSymmetric[{s1,…,sn}]零张量的对称性
  • 可以给出下列选项：
  • Assumptions$Assumptions关于张量的假设
    SameTestAutomatic测试表达式的相等性的函数
    ToleranceAutomatic近似数字的容差
  • 对于精确的符号数组，选项 SameTest->f 表示如果 f[aij…,akl…] 给出 True，则 aij… 和 akl… 被视为相等.
  • 对于近似数组，选项 Tolerance->t 可用来表示把所有的项 Abs[aij…]≤t 视为零.
  • 对于数组中的项 Abs[aij…]>t，比较相等性时不考虑最后 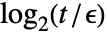位，其中，对于 MachinePrecision 数组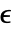， 为 $MachineEpsilon，对于 Precision 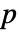的数组为 .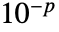

范例

打开所有单元关闭所有单元

基本范例  (2)常见实例总结

对称矩阵：

In[1]:=1
✖
https://wolfram.com/xid/0rsy8amms-l1jrsp
Out[1]=1

反对称矩阵：

In[2]:=2
✖
https://wolfram.com/xid/0rsy8amms-le6d13
Out[2]=2

阶数为3的对称数组：

In[1]:=1
✖
https://wolfram.com/xid/0rsy8amms-6qgilb
In[2]:=2
✖
https://wolfram.com/xid/0rsy8amms-82w844
Out[2]=2

范围  (7)标准用法实例范围调查

求数组中的对称性：

In[1]:=1
✖
https://wolfram.com/xid/0rsy8amms-dbf8n0
Out[1]=1

求复数组的对称性：

In[1]:=1
✖
https://wolfram.com/xid/0rsy8amms-u796hm
Out[1]=1

SymmetrizedArray 对象的对称性：

In[1]:=1
✖
https://wolfram.com/xid/0rsy8amms-lzpcun
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0rsy8amms-2tswmd
Out[2]=2

SparseArray 对象的对称性：

In[1]:=1
✖
https://wolfram.com/xid/0rsy8amms-gluuys
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0rsy8amms-ecq6v7
Out[2]=2

指定符号式数组的对称性：

In[1]:=1
✖
https://wolfram.com/xid/0rsy8amms-z2l6p6
In[2]:=2
✖
https://wolfram.com/xid/0rsy8amms-gnqc9d
Out[2]=2

张量与自身乘积的对称性. 注意交换对称性：

In[3]:=3
✖
https://wolfram.com/xid/0rsy8amms-4mnhck
Out[3]=3

完全对称的阶数为3的数组：

In[1]:=1
✖
https://wolfram.com/xid/0rsy8amms-cixa42
Out[1]=1

完全对称性：

In[2]:=2
✖
https://wolfram.com/xid/0rsy8amms-f2c8kg
Out[2]=2

在位置子集中的对称性：

In[3]:=3
✖
https://wolfram.com/xid/0rsy8amms-1z9c3k
Out[3]=3

由零组成的数组的对称性：

In[1]:=1
✖
https://wolfram.com/xid/0rsy8amms-fejnuo
Out[1]=1

选项  (3)各选项的常用值和功能

Assumptions  (1)

局部指定张量属性：

In[1]:=1
✖
https://wolfram.com/xid/0rsy8amms-lr5mpx
Out[1]=1

在没有假定的情况下，对称性未知：

In[2]:=2
✖
https://wolfram.com/xid/0rsy8amms-thdqaj
Out[2]=2

SameTest  (1)

下面的矩阵对于正实数 是对称的，但是 TensorSymmetry 给出的结果是不对称：

In[1]:=1
✖
https://wolfram.com/xid/0rsy8amms-tc73f
In[2]:=2
✖
https://wolfram.com/xid/0rsy8amms-e6d7o
Out[2]=2

用选项 SameTest 获得正确的答案：

In[3]:=3
✖
https://wolfram.com/xid/0rsy8amms-mcli5n
Out[3]=3

Tolerance  (1)

生成深度为 4 的全对称随机数组：

In[1]:=1
✖
https://wolfram.com/xid/0rsy8amms-cbl75w
In[2]:=2
✖
https://wolfram.com/xid/0rsy8amms-bv39ow
In[3]:=3
✖
https://wolfram.com/xid/0rsy8amms-kgjw4g
Out[3]=3

添加一个很小的干扰就破坏了对称性：

In[4]:=4
✖
https://wolfram.com/xid/0rsy8amms-jgtn97
In[5]:=5
✖
https://wolfram.com/xid/0rsy8amms-dzdiny
Out[5]=5

允许一定的容差，即可恢复对称性：

In[6]:=6
✖
https://wolfram.com/xid/0rsy8amms-0ut4o
Out[6]=6

属性和关系  (5)函数的属性及与其他函数的关联

测试一个矩阵是否是对称的：

In[1]:=1
✖
https://wolfram.com/xid/0rsy8amms-cqwyim
In[2]:=2
✖
https://wolfram.com/xid/0rsy8amms-eg0e38
Out[2]=2

给出矩阵的对称性：

In[3]:=3
✖
https://wolfram.com/xid/0rsy8amms-lmny8
Out[3]=3

测试一个矩阵是否是反对称的：

In[1]:=1
✖
https://wolfram.com/xid/0rsy8amms-nzh81
In[2]:=2
✖
https://wolfram.com/xid/0rsy8amms-4t0ij
Out[2]=2

给出矩阵的对称性：

In[3]:=3
✖
https://wolfram.com/xid/0rsy8amms-dcgx07
Out[3]=3

只有零矩阵可以同时具有对称性和反对称性：

In[1]:=1
✖
https://wolfram.com/xid/0rsy8amms-344fx
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0rsy8amms-pm1kl
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0rsy8amms-d5nfkw
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0rsy8amms-ocrzq
Out[4]=4

特殊多维对称数组的生成：

In[1]:=1
✖
https://wolfram.com/xid/0rsy8amms-kgrwe2
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0rsy8amms-b3k6pu
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0rsy8amms-k3ejp4
Out[3]=3

在不同的半径下，存在其他对称性：

In[4]:=4
✖
https://wolfram.com/xid/0rsy8amms-idgrpv
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0rsy8amms-0in36m
Out[5]=5

Symmetrize[tensor,sym] 的对称性至少是 sym：

In[1]:=1
✖
https://wolfram.com/xid/0rsy8amms-im2xss
In[2]:=2
✖
https://wolfram.com/xid/0rsy8amms-izaw5s
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0rsy8amms-fpl3ao
Out[3]=3

有些情况下，Symmetrize[tensor,sym] 的结果给出的对称性可能要大于 sym：

In[4]:=4
✖
https://wolfram.com/xid/0rsy8amms-c9fmbr
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0rsy8amms-hpsz0j
Out[5]=5
Wolfram Research (2012)，TensorSymmetry，Wolfram 语言函数，https://reference.wolfram.com/language/ref/TensorSymmetry.html （更新于 2017 年）.
✖
Wolfram Research (2012)，TensorSymmetry，Wolfram 语言函数，https://reference.wolfram.com/language/ref/TensorSymmetry.html （更新于 2017 年）.

文本

Wolfram Research (2012)，TensorSymmetry，Wolfram 语言函数，https://reference.wolfram.com/language/ref/TensorSymmetry.html （更新于 2017 年）.

✖
Wolfram Research (2012)，TensorSymmetry，Wolfram 语言函数，https://reference.wolfram.com/language/ref/TensorSymmetry.html （更新于 2017 年）.

CMS

Wolfram 语言. 2012. "TensorSymmetry." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2017. https://reference.wolfram.com/language/ref/TensorSymmetry.html.

✖
Wolfram 语言. 2012. "TensorSymmetry." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2017. https://reference.wolfram.com/language/ref/TensorSymmetry.html.

APA

Wolfram 语言. (2012). TensorSymmetry. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/TensorSymmetry.html 年

✖
Wolfram 语言. (2012). TensorSymmetry. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/TensorSymmetry.html 年

BibTeX

@misc{reference.wolfram_2025_tensorsymmetry, author="Wolfram Research", title="{TensorSymmetry}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/TensorSymmetry.html}", note=[Accessed: 06-April-2025 ]}

✖
@misc{reference.wolfram_2025_tensorsymmetry, author="Wolfram Research", title="{TensorSymmetry}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/TensorSymmetry.html}", note=[Accessed: 06-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_tensorsymmetry, organization={Wolfram Research}, title={TensorSymmetry}, year={2017}, url={https://reference.wolfram.com/language/ref/TensorSymmetry.html}, note=[Accessed: 06-April-2025 ]}

✖
@online{reference.wolfram_2025_tensorsymmetry, organization={Wolfram Research}, title={TensorSymmetry}, year={2017}, url={https://reference.wolfram.com/language/ref/TensorSymmetry.html}, note=[Accessed: 06-April-2025 ]}