Torus

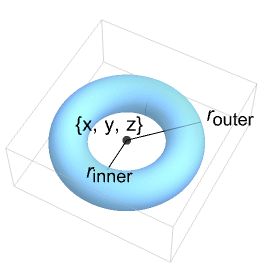
Torus[{x,y,z},{rinner,router}]

represents a torus centered at {x,y,z} with inner radius rinner and outer radius router.

Details and Options

  • Torus is also known as torus of revolution.
  • Torus can be used as a geometric region and a 3D graphics primitive.
  • Torus[] is equivalent to Torus[{0,0,0},{1/2,1}].
  • Torus represents the shell .
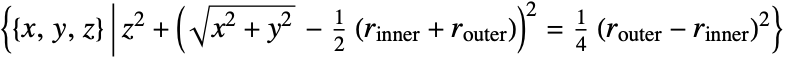  • Torus can be used in Graphics3D.
  • Graphics rendering is affected by directives such as FaceForm, Specularity, Opacity and color.

Examples

open allclose all

Basic Examples  (2)

A standard torus at the origin:

Area and centroid:

Scope  (18)

Graphics  (9)

Specification  (4)

The standard torus:

Filled tori with different outer radii:

Filled tori with different inner radii:

Short form for a torus with radii at the origin:

Styling  (4)

Colored tori:

Different properties can be specified for the front and back of faces using FaceForm:

Filled tori with different specular exponents:

White torus that glows red:

Opacity specifies the face opacity:

Coordinates  (1)

Points can be Dynamic:

Regions  (9)

Embedding dimension is the dimension of the space in which the torus lives:

Geometric dimension is the dimension of the shape itself:

Membership testing:

Get conditions for point membership:

Area:

Centroid:

Distance from a point:

The equidistance contours for a torus:

Signed distance from a point:

Nearest point in the region:

Nearest points to an enclosing sphere:

A torus is bounded:

Find its range:

Optimize over a torus region:

Solve equations in a torus region:

Applications  (2)

Bubbles:

Use Torus to render nodes in a GraphPlot3D:

Properties & Relations  (3)

An implicit specification of a torus generated by ContourPlot3D:

A parametric specification of a torus generated by ParametricPlot3D:

Torus is the RegionBoundary of FilledTorus:

Neat Examples  (3)

Random torus collections:

Double helix:

Nested tori:

Wolfram Research (2021), Torus, Wolfram Language function, https://reference.wolfram.com/language/ref/Torus.html.

Text

Wolfram Research (2021), Torus, Wolfram Language function, https://reference.wolfram.com/language/ref/Torus.html.

CMS

Wolfram Language. 2021. "Torus." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Torus.html.

APA

Wolfram Language. (2021). Torus. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Torus.html

BibTeX

@misc{reference.wolfram_2025_torus, author="Wolfram Research", title="{Torus}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/Torus.html}", note=[Accessed: 21-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_torus, organization={Wolfram Research}, title={Torus}, year={2021}, url={https://reference.wolfram.com/language/ref/Torus.html}, note=[Accessed: 21-February-2025 ]}