represents a Tracy–Widom distribution with Dyson index β.


TracyWidomDistribution
represents a Tracy–Widom distribution with Dyson index β.
Details
- The Tracy–Widom distribution is the limiting probability distribution of the normalized largest eigenvalue of a random matrix that belongs to a Gaussian ensemble.
- TracyWidomDistribution allows the Dyson index β to be 1, 2, or 4 according to the underlying matrix distribution:
-
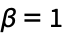
GaussianOrthogonalMatrixDistribution β2 GaussianUnitaryMatrixDistribution β4 GaussianSymplecticMatrixDistribution - TracyWidomDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Examples
open all close allBasic Examples (4)
Scope (4)
Applications (4)
Use MatrixPropertyDistribution to represent the normalized largest eigenvalue of a matrix from Gaussian unitary ensemble:
Sample from MatrixPropertyDistribution:
Compare the histogram with the PDF:
Perform similar computations with Gaussian orthogonal ensemble and Gaussian symplectic ensemble:
Compare the histograms with the PDFs:
When n and p (the dimension of the covariance matrix Σ) are both large, the scaled largest eigenvalue of a matrix from Wishart ensemble with identity covariance is approximately distributed as Tracy–Widom distribution of ![]() :
:
Sample the scaled largest eigenvalue:
Compare the histogram of scaled largest eigenvalues with the PDF:
Compare the CDFs of Tracy–Widom distributions with the leading order asymptotic expansion on the left tail in log scale:
Define a function to find the length of LongestOrderedSequence in the given sequence:
Find lengths of the longest increasing subsequence in random permutations of list ![]() :
:
Compare the scaled length of the longest increasing subsequence with Tracy–Widom distribution of ![]() :
:
Properties & Relations (2)
CDFs of Tracy–Widom distributions for different values of β are related to each other:
Tracy–Widom distributions can be well approximated by GammaDistribution in the central region:
Match GammaDistribution with Tracy–Widom distribution of ![]() with the first three moments:
with the first three moments:
Related Guides
History
Text
Wolfram Research (2015), TracyWidomDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/TracyWidomDistribution.html.
CMS
Wolfram Language. 2015. "TracyWidomDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TracyWidomDistribution.html.
APA
Wolfram Language. (2015). TracyWidomDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TracyWidomDistribution.html
BibTeX
@misc{reference.wolfram_2025_tracywidomdistribution, author="Wolfram Research", title="{TracyWidomDistribution}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/TracyWidomDistribution.html}", note=[Accessed: 01-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_tracywidomdistribution, organization={Wolfram Research}, title={TracyWidomDistribution}, year={2015}, url={https://reference.wolfram.com/language/ref/TracyWidomDistribution.html}, note=[Accessed: 01-January-2026]}