GaussianSymplecticMatrixDistribution
GaussianSymplecticMatrixDistribution[σ,n]
represents a Gaussian symplectic matrix distribution with matrix dimensions {2 n,2 n} over the field of complex numbers and scale parameter σ.
GaussianSymplecticMatrixDistribution[n]
represents a Gaussian symplectic matrix distribution with unit scale parameter.
Details
- GaussianSymplecticMatrixDistribution is also known as Gaussian symplectic ensemble, or GSE.
- GaussianSymplecticMatrixDistribution is a distribution of symplectic Hermitian matrix
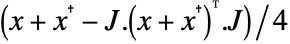, where 
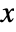is a complex square matrix with independent identically distributed real and imaginary matrix elements that follow NormalDistribution[0,σ], and where 
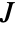is the skew‐symmetric matrix KroneckerProduct[{{0,-1},{1,0}},IdentityMatrix[n]]. - Quaternion Hermitian matrix
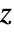in a Gaussian symplectic matrix distribution has the block structure 
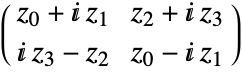, where 
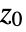is a real symmetric matrix with matrix dimensions {n,n}, and 
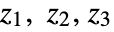are real anti-symmetric matrices with matrix dimensions {n,n}. - The probability density for
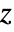is proportional to 
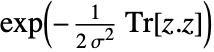. - The scale parameter σ can be any positive number and dimension parameter n can be any positive integer.
- GaussianSymplecticMatrixDistribution can be used with such functions as MatrixPropertyDistribution, EstimatedDistribution, and RandomVariate.
Background & Context
- GaussianSymplecticMatrixDistribution[σ,n], also referred to as a Gaussian symplectic ensemble (GSE), represents a statistical distribution over the
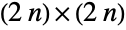complex symplectic Hermitian matrices, namely square complex matrices 
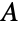of even dimension that satisfy both 
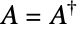and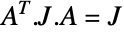 
, where 
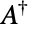denotes the conjugate transpose of 
, 
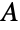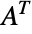the transpose of 
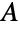and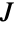 
is a symplectic matrix of the form 
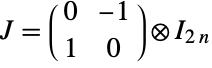with ⊗ the Kronecker product. Matrices 
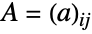distributed according to GaussianSymplecticMatrixDistribution have probability densities proportional to 
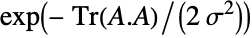. Furthermore, the collection 
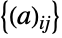of all entries is an independent collection of complex variates whose real and imaginary parts (Re and Im, respectively) are distributed identically according to NormalDistribution[0,σ]. GaussianSymplecticMatrixDistribution[σ,n] is parameterized by a positive integer n (the dimension parameter) and by a positive real number σ (the scale parameter). Despite the name "Gaussian symplectic matrix distribution", matrices belonging to this distribution need not be symplectic. - The one-parameter form GaussianSymplecticMatrixDistribution[n] is equivalent to GaussianSymplecticMatrixDistribution[1,n].
- Along with the Gaussian orthogonal and Gaussian unitary ensembles (GaussianOrthogonalMatrixDistribution and GaussianUnitaryMatrixDistribution, respectively), the Gaussian symplectic matrix distribution was one of three Gaussian matrix ensembles originally suggested by Eugene Wigner as a tool to study fluctuations in nuclear physics. Mathematically, the GSE is invariant under conjugation by elements of the symplectic group, while physically modeling Hamiltonians with time-reversal symmetry but with no rotational symmetry. Matrix ensembles like the Gaussian symplectic matrix distribution are of considerable importance in the study of random matrix theory, as well as in various branches of physics and mathematics.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Gaussian symplectic matrix distribution, and the mean, median, variance, raw moments and central moments of a collection of such variates may then be computed using Mean, Median, Variance, Moment and CentralMoment, respectively. Distributed[A,GaussianSymplecticMatrixDistribution[σ,n]], written more concisely as AGaussianSymplecticMatrixDistribution[σ,n], can be used to assert that a random matrix A is distributed according to a Gaussian symplectic distribution. Such an assertion can then be used in functions such as MatrixPropertyDistribution.
- The trace, eigenvalues and norm of variates distributed according to Gaussian symplectic matrix distribution may be computed using Tr, Eigenvalues and Norm, respectively. Such variates may also be examined with MatrixFunction, MatrixPower, and real quantities related thereto, such as the real part (Re), imaginary part (Im) and complex argument (Arg), can be plotted using MatrixPlot.
- GaussianSymplecticMatrixDistribution is related to a number of other distributions. As discussed above, it is qualitatively similar to other Gaussian matrix distributions GaussianOrthogonalMatrixDistribution and GaussianUnitaryMatrixDistribution. Generalizations of the Gaussian ensembles include the so-called circular matrix ensembles, and so GaussianSymplecticMatrixDistribution is also related to CircularOrthogonalMatrixDistribution, CircularQuaternionMatrixDistribution, CircularRealMatrixDistribution, CircularSymplecticMatrixDistribution and CircularUnitaryMatrixDistribution. GaussianSymplecticMatrixDistribution is also related to MatrixNormalDistribution, MatrixTDistribution, WishartMatrixDistribution, InverseWishartMatrixDistribution, TracyWidomDistribution and WignerSemicircleDistribution.
Examples
open allclose allBasic Examples (3)
Generate a pseudorandom matrix:
Check that the matrix is Hermitian:
Check that is also quaternion self‐dual:
Represent the joint distribution of eigenvalues of a random matrix by MatrixPropertyDistribution and sample from it:
Scope (4)
Generate a single pseudorandom matrix:
Generate a set of pseudorandom matrices:
Compute statistical properties numerically:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare LogLikelihood of the distributions:
Applications (2)
Sample eigenvalue spacing distribution in a 2‐by‐2 GSE matrix:
Compare the histogram with the closed form, also known as Wigner surmise for Dyson index 
:
Sample the joint distribution of eigenvalues of 2-by-2 GSE matrix:
Generically, eigenvalues have multiplicity 2:
Use RandomSample to randomly permute eigenvalues to compensate for algorithm‐specific ordering:
Compare the estimated density to the known closed form result:
Evaluate the density for the case of 2-by-2 GSE matrices:
Compare the density to the histogram density estimate from the sample:
Properties & Relations (4)
Each realization of GaussianSymplecticMatrixDistribution is a Hermitian matrix:
Furthermore, a sample matrix from GaussianSymplecticMatrixDistribution satisfies quaternion self-duality condition:
MatrixExp applied to 
with 
sampled from GaussianSymplecticMatrixDistribution is unitary symplectic matrix:
Spectral density of large GSE matrix converges to WignerSemicircleDistribution:
Compare the histogram with the PDF:
The distribution of scaled largest eigenvalue of large GSE matrices converges to TracyWidomDistribution:
Compare sample histogram with the PDF of TracyWidomDistribution[4]:
Text
Wolfram Research (2015), GaussianSymplecticMatrixDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/GaussianSymplecticMatrixDistribution.html (updated 2017).
CMS
Wolfram Language. 2015. "GaussianSymplecticMatrixDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/GaussianSymplecticMatrixDistribution.html.
APA
Wolfram Language. (2015). GaussianSymplecticMatrixDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GaussianSymplecticMatrixDistribution.html