CircularUnitaryMatrixDistribution[n]
represents a circular unitary matrix distribution with matrix dimensions {n,n}.


CircularUnitaryMatrixDistribution
CircularUnitaryMatrixDistribution[n]
represents a circular unitary matrix distribution with matrix dimensions {n,n}.
Details
- CircularUnitaryMatrixDistribution is also known as circular unitary ensemble, or CUE.
- CircularUnitaryMatrixDistribution represents a uniform distribution over the unitary square matrices of dimension n, also known as the Haar measure on the unitary group
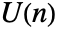 .
. - The dimension parameter n can be any positive integer.
- CircularUnitaryMatrixDistribution can be used with such functions as MatrixPropertyDistribution and RandomVariate.
Background & Context
- CircularUnitaryMatrixDistribution[n], also referred to as the circular unitary ensemble (CUE), represents a statistical distribution over the
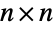 unitary complex matrices, namely complex square matrices
unitary complex matrices, namely complex square matrices 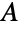 satisfying
satisfying 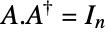 , where
, where 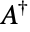 denotes the conjugate transpose of
denotes the conjugate transpose of 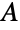 and
and 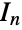 the
the 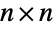 identity matrix. The parameter n is called the dimension parameter of the distribution and may be any positive integer.
identity matrix. The parameter n is called the dimension parameter of the distribution and may be any positive integer. - Along with the circular symplectic and circular orthogonal matrix distributions (CircularSymplecticMatrixDistribution and CircularOrthogonalMatrixDistribution, respectively), the circular unitary matrix distribution was one of three so-called circle matrix ensembles originally devised by Freeman Dyson in 1962 as a tool to study quantum mechanics. Probabilistically, the circular unitary matrix distribution represents a uniform distribution over the unitary square matrices, while mathematically it is a so-called Haar measure on the unitary group
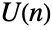 . Matrix ensembles like the circular unitary matrix distribution are of considerable importance in the study of random matrix theory, as well as in various branches of physics and mathematics.
. Matrix ensembles like the circular unitary matrix distribution are of considerable importance in the study of random matrix theory, as well as in various branches of physics and mathematics. - RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a circular unitary matrix distribution, and the mean, median, variance, raw moments and central moments of a collection of such variates may then be computed using Mean, Median, Variance, Moment and CentralMoment, respectively. Distributed[A,CircularUnitaryMatrixDistribution[n]], written more concisely as ACircularUnitaryMatrixDistribution[n], can be used to assert that a random matrix A is distributed according to a circular unitary matrix distribution. Such an assertion can then be used in functions such as MatrixPropertyDistribution.
- The trace, eigenvalues and norm of variates distributed according to circular unitary matrix distribution may be computed using Tr, Eigenvalues and Norm, respectively. Such variates may also be examined with MatrixFunction, MatrixPower, and real quantities related thereto, such as the real part (Re), imaginary part (Im) and complex argument (Arg), can be plotted using MatrixPlot.
- CircularUnitaryMatrixDistribution is related to a number of other distributions. As discussed above, it is qualitatively similar to other circular matrix distributions such as CircularQuaternionMatrixDistribution, CircularRealMatrixDistribution, CircularSymplecticMatrixDistribution and CircularOrthogonalMatrixDistribution. Originally, the circular matrix ensembles were derived as generalizations of the so-called Gaussian ensembles, and so CircularUnitaryMatrixDistribution is related to GaussianOrthogonalMatrixDistribution, GaussianSymplecticMatrixDistribution and GaussianUnitaryMatrixDistribution. CircularUnitaryMatrixDistribution is also related to MatrixNormalDistribution, MatrixTDistribution, WishartMatrixDistribution, InverseWishartMatrixDistribution, TracyWidomDistribution and WignerSemicircleDistribution.
Examples
open all close allBasic Examples (2)
Verify that the matrix is unitary:
Represent the eigenvalues of a random matrix by MatrixPropertyDistribution and sample from it:
Scope (3)
Applications (4)
Define distribution of complex arguments of random matrix eigenvalues:
Sample the phases of eigenvalues followed by random permutations:
Visualize joint phase distribution together with the closed form PDF:
The number of permutations ![]() of
of ![]() elements in which the longest increasing subsequence is at most of length
elements in which the longest increasing subsequence is at most of length ![]() can computed by averaging over
can computed by averaging over ![]() , where
, where ![]() are drawn from CircularUnitaryMatrixDistribution[n]:
are drawn from CircularUnitaryMatrixDistribution[n]:
The joint distribution of the eigenvalues for CircularUnitaryMatrixDistribution is also Boltzmann distribution of Dyson's Coulomb gas on a circle with inverse temperature ![]() . The average Hamiltonian per particle of the system is (without kinetic terms):
. The average Hamiltonian per particle of the system is (without kinetic terms):
Define the distribution of the value of the Hamiltonian on random CUE matrix:
Compute the sample mean of the Hamiltonian for systems of different size:
Plot the sample means and compare them with thermodynamic limit:
Construct Brownian motion on CUE by using matrices from GaussianUnitaryMatrixDistribution as infinitesimal generators:
Generate a Brownian path with initial matrix sampled from CircularUnitaryMatrixDistribution:
Compute the phase of the eigenvalues and compare them with the PDF of the eigenvalues of matrices from CircularUnitaryMatrixDistribution:
Properties & Relations (2)
Distribution of phase angle of the eigenvalues:
Compute the spacing between eigenvalues:
Compare the histogram of sample level spacings with the closed form, also known as Wigner surmise for Dyson index 2:
For eigenvectors of CircularUnitaryMatrixDistribution with dimension ![]() large, the scaled modulus of the elements is
large, the scaled modulus of the elements is ![]() distributed:
distributed:
Compare the histogram with PDF of ChiSquareDistribution:
Related Guides
History
Text
Wolfram Research (2015), CircularUnitaryMatrixDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/CircularUnitaryMatrixDistribution.html.
CMS
Wolfram Language. 2015. "CircularUnitaryMatrixDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CircularUnitaryMatrixDistribution.html.
APA
Wolfram Language. (2015). CircularUnitaryMatrixDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CircularUnitaryMatrixDistribution.html
BibTeX
@misc{reference.wolfram_2025_circularunitarymatrixdistribution, author="Wolfram Research", title="{CircularUnitaryMatrixDistribution}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/CircularUnitaryMatrixDistribution.html}", note=[Accessed: 15-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_circularunitarymatrixdistribution, organization={Wolfram Research}, title={CircularUnitaryMatrixDistribution}, year={2015}, url={https://reference.wolfram.com/language/ref/CircularUnitaryMatrixDistribution.html}, note=[Accessed: 15-February-2026]}