CircularQuaternionMatrixDistribution[n]
represents a circular quaternion matrix distribution with matrix dimensions {2 n,2 n} over the field of complex numbers.


CircularQuaternionMatrixDistribution
CircularQuaternionMatrixDistribution[n]
represents a circular quaternion matrix distribution with matrix dimensions {2 n,2 n} over the field of complex numbers.
Details
- CircularQuaternionMatrixDistribution is also known as circular quaternion ensemble, or CQE.
- CircularQuaternionMatrixDistribution represents a uniform distribution over the compact symplectic square matrices of dimension n. It is also known as the Haar measure on the unitary symplectic group
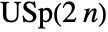 .
. - Each realization of CircularQuaternionMatrixDistribution is represented as a unitary matrix
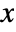 that preserves the symplectic form
that preserves the symplectic form ![TemplateBox[{x}, Transpose].J.x=J TemplateBox[{x}, Transpose].J.x=J](Files/CircularQuaternionMatrixDistribution.en/3.png) , where
, where 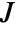 is a symplectic matrix KroneckerProduct[{{0,-1},{1,0}},IdentityMatrix[n]].
is a symplectic matrix KroneckerProduct[{{0,-1},{1,0}},IdentityMatrix[n]]. - The dimension parameter n can be any positive integer.
- CircularQuaternionMatrixDistribution can be used with such functions as MatrixPropertyDistribution and RandomVariate.
Background & Context
- CircularQuaternionMatrixDistribution[n], also referred to as the circular quaternion ensemble (CQE), represents a statistical distribution over the
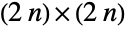 unitary complex matrices, namely complex matrices
unitary complex matrices, namely complex matrices 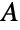 of even dimension satisfying both
of even dimension satisfying both 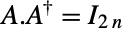 and
and 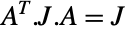 , where
, where 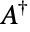 denotes the conjugate transpose of
denotes the conjugate transpose of 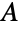 ,
, 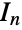 the
the 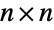 identity matrix,
identity matrix, 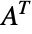 the transpose of
the transpose of 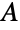 and
and 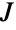 is a symplectic matrix of the form
is a symplectic matrix of the form 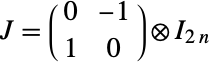 with ⊗ the Kronecker product. The parameter n is called the dimension parameter of the distribution and may be any positive integer.
with ⊗ the Kronecker product. The parameter n is called the dimension parameter of the distribution and may be any positive integer. - Along with the circular real matrix ensemble (CircularRealMatrixDistribution), the circular quaternion matrix distribution is one of two major additions to the three original so-called circle matrix ensembles (CircularOrthogonalMatrixDistribution, CircularSymplecticMatrixDistribution and CircularUnitaryMatrixDistribution) devised by Freeman Dyson in 1962. Probabilistically, the circular quaternion matrix distribution represents a uniform distribution over the collection of compact symplectic square matrices, while mathematically it is a so-called Haar measure on the unitary symplectic group
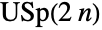 . Matrix ensembles like the circular quaternion matrix distribution are of considerable importance in the study of random matrix theory, as well as in various branches of physics and mathematics.
. Matrix ensembles like the circular quaternion matrix distribution are of considerable importance in the study of random matrix theory, as well as in various branches of physics and mathematics. - RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a circular quaternion matrix distribution, and the mean, median, variance, raw moments and central moments of a collection of such variates may then be computed using Mean, Median, Variance, Moment and CentralMoment, respectively. Distributed[A,CircularQuaternionMatrixDistribution[n]], written more concisely as ACircularQuaternionMatrixDistribution[n], can be used to assert that a random matrix A is distributed according to a circular quaternion matrix distribution. Such an assertion can then be used in functions such as MatrixPropertyDistribution.
- The trace, eigenvalues and norm of variates distributed according to circular quaternion matrix distribution may be computed using Tr, Eigenvalues and Norm, respectively. Such variates may also be examined with MatrixFunction, MatrixPower, and real quantities related thereto, such as the real part (Re), imaginary part (Im) and complex argument (Arg), can be plotted using MatrixPlot.
- CircularQuaternionMatrixDistribution is related to a number of other distributions. As discussed above, it is qualitatively similar to other circular matrix distributions such as CircularOrthogonalMatrixDistribution, CircularRealMatrixDistribution, CircularSymplecticMatrixDistribution and CircularUnitaryMatrixDistribution. Originally, the circular matrix ensembles were derived as generalizations of the so-called Gaussian ensembles, and so CircularQuaternionMatrixDistribution is related to GaussianOrthogonalMatrixDistribution, GaussianSymplecticMatrixDistribution and GaussianUnitaryMatrixDistribution. CircularQuaternionMatrixDistribution is also related to MatrixNormalDistribution, MatrixTDistribution, WishartMatrixDistribution, InverseWishartMatrixDistribution, TracyWidomDistribution and WignerSemicircleDistribution.
Examples
open all close allBasic Examples (2)
Generate a pseudorandom CQE matrix:
It is unitary and preserves the symplectic matrix :
Represent the eigenvalues of a random matrix by MatrixPropertyDistribution and sample from it:
Scope (3)
Properties & Relations (2)
Distribution of phase angle of the eigenvalues:
Compute the spacing between eigenvalues:
Compare the histogram of sample level spacings with the closed form, also known as Wigner surmise for Dyson index 2:
For eigenvectors of CircularQuaternionMatrixDistribution with dimension ![]() large, the scaled modulus of the elements is
large, the scaled modulus of the elements is ![]() distributed:
distributed:
Compare the histogram with PDF of ChiSquareDistribution:
Related Guides
History
Text
Wolfram Research (2015), CircularQuaternionMatrixDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/CircularQuaternionMatrixDistribution.html.
CMS
Wolfram Language. 2015. "CircularQuaternionMatrixDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CircularQuaternionMatrixDistribution.html.
APA
Wolfram Language. (2015). CircularQuaternionMatrixDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CircularQuaternionMatrixDistribution.html
BibTeX
@misc{reference.wolfram_2025_circularquaternionmatrixdistribution, author="Wolfram Research", title="{CircularQuaternionMatrixDistribution}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/CircularQuaternionMatrixDistribution.html}", note=[Accessed: 11-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_circularquaternionmatrixdistribution, organization={Wolfram Research}, title={CircularQuaternionMatrixDistribution}, year={2015}, url={https://reference.wolfram.com/language/ref/CircularQuaternionMatrixDistribution.html}, note=[Accessed: 11-March-2026]}