GaussianUnitaryMatrixDistribution[σ,n]
represents a Gaussian unitary matrix distribution with matrix dimensions {n,n} and scale parameter σ.
GaussianUnitaryMatrixDistribution[n]
represents a Gaussian unitary matrix distribution with unit scale parameter.


GaussianUnitaryMatrixDistribution
GaussianUnitaryMatrixDistribution[σ,n]
represents a Gaussian unitary matrix distribution with matrix dimensions {n,n} and scale parameter σ.
GaussianUnitaryMatrixDistribution[n]
represents a Gaussian unitary matrix distribution with unit scale parameter.
Details
- GaussianUnitaryMatrixDistribution is also known as Gaussian unitary ensemble, or GUE.
- GaussianUnitaryMatrixDistribution is a distribution of a Hermitian matrix
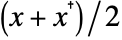 , where
, where 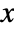 is a complex square matrix with independent identically distributed real and imaginary matrix elements that follow NormalDistribution[0,σ].
is a complex square matrix with independent identically distributed real and imaginary matrix elements that follow NormalDistribution[0,σ]. - The probability density for
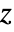 is proportional to
is proportional to 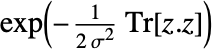 .
. - The scale parameter σ can be any positive number and n can be any positive integer.
- GaussianUnitaryMatrixDistribution can be used with such functions as MatrixPropertyDistribution, EstimatedDistribution, and RandomVariate.
Background & Context
- GaussianUnitaryMatrixDistribution[σ,n], also referred to as a Gaussian unitary ensemble (GUE), represents a statistical distribution over the
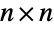 complex Hermitian matrices, namely square complex matrices
complex Hermitian matrices, namely square complex matrices 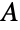 that satisfy
that satisfy 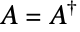 , where
, where 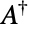 denotes the conjugate transpose of
denotes the conjugate transpose of 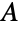 . Matrices
. Matrices 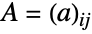 distributed according to GaussianUnitaryMatrixDistribution have probability densities proportional to
distributed according to GaussianUnitaryMatrixDistribution have probability densities proportional to 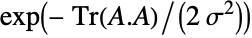 . Furthermore, the collection
. Furthermore, the collection 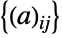 of all entries is an independent collection of complex variates whose real and imaginary parts (Re and Im, respectively) are distributed identically according to NormalDistribution[0,σ]. GaussianUnitaryMatrixDistribution[σ,n] is parameterized by a positive integer n (the dimension parameter) and a positive real number σ (the scale parameter). Despite the name "Gaussian unitary matrix distribution", matrices belonging to this distribution need not be unitary.
of all entries is an independent collection of complex variates whose real and imaginary parts (Re and Im, respectively) are distributed identically according to NormalDistribution[0,σ]. GaussianUnitaryMatrixDistribution[σ,n] is parameterized by a positive integer n (the dimension parameter) and a positive real number σ (the scale parameter). Despite the name "Gaussian unitary matrix distribution", matrices belonging to this distribution need not be unitary. - The one-parameter form GaussianUnitaryMatrixDistribution[n] is equivalent to GaussianUnitaryMatrixDistribution[1,n].
- Along with the Gaussian orthogonal and Gaussian symplectic ensembles (GaussianOrthogonalMatrixDistribution and GaussianSymplecticMatrixDistribution, respectively), the Gaussian unitary matrix distribution was one of three Gaussian matrix ensembles originally suggested by Eugene Wigner as a tool to study fluctuations in nuclear physics. Mathematically, the GUE is invariant under conjugation by unitary matrices, while physically modeling Hamiltonians lacking time-reversal symmetry. Matrix ensembles like the Gaussian unitary matrix distribution are of considerable importance in the study of random matrix theory, as well as in various branches of physics and mathematics.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Gaussian unitary matrix distribution, and the mean, median, variance, raw moments and central moments of a collection of such variates may then be computed using Mean, Median, Variance, Moment and CentralMoment, respectively. Distributed[A,GaussianUnitaryMatrixDistribution[σ,n]], written more concisely as AGaussianUnitaryMatrixDistribution[σ,n], can be used to assert that a random matrix A is distributed according to a Gaussian unitary matrix distribution. Such an assertion can then be used in functions such as MatrixPropertyDistribution.
- The trace, eigenvalues and norm of variates distributed according to Gaussian unitary matrix distribution may be computed using Tr, Eigenvalues and Norm, respectively. Such variates may also be examined with MatrixFunction, MatrixPower and real quantities related thereto, such as the real part (Re), imaginary part (Im) and complex argument (Arg), can be plotted using MatrixPlot.
- GaussianUnitaryMatrixDistribution is related to a number of other distributions. As discussed above, it is qualitatively similar to other Gaussian matrix distributions GaussianOrthogonalMatrixDistribution and GaussianSymplecticMatrixDistribution. Generalizations of the Gaussian ensembles include the so-called circular matrix ensembles, and so GaussianUnitaryMatrixDistribution is also related to CircularOrthogonalMatrixDistribution, CircularQuaternionMatrixDistribution, CircularRealMatrixDistribution, CircularSymplecticMatrixDistribution and CircularUnitaryMatrixDistribution. GaussianUnitaryMatrixDistribution is also related to MatrixNormalDistribution, MatrixTDistribution, WishartMatrixDistribution, InverseWishartMatrixDistribution, TracyWidomDistribution and WignerSemicircleDistribution.
Examples
open all close allBasic Examples (4)
Generate a pseudorandom GUE matrix:
Independent real components of a matrix from GaussianUnitaryMatrixDistribution are jointly Gaussian, uncorrelated, with entries off the diagonal having half the variance of entries on the diagonal:
Use MatrixPropertyDistribution to sample eigenvalues of GUE matrices:
Scope (4)
Generate a single pseudorandom matrix:
Generate a set of pseudorandom matrices:
Compute statistical properties numerically:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare LogLikelihood of the distributions:
Applications (3)
Sample eigenvalue spacing distribution in a 2‐by‐2 GUE matrix:
Compare the histogram with the closed form, also known as Wigner surmise for Dyson index ![]() :
:
Sample the joint distribution of eigenvalues of 2-by-2 GUE matrix:
Use RandomSample to randomly permute eigenvalues to compensate for algorithm‐specific ordering:
Compare the estimated density to the known closed form result:
Evaluate the density for the case of 2-by-2 GUE matrices:
Compare the density to the histogram density estimate from the sample:
Confirm the agreement with a goodness-of-fit test:
Construct Brownian motion on CUE by using matrices from GaussianUnitaryMatrixDistribution as infinitesimal generators:
Generate a Brownian path with initial matrix sampled from CircularUnitaryMatrixDistribution:
Compute the phase of the eigenvalues and compare them with the PDF of the eigenvalues of matrices from CircularUnitaryMatrixDistribution:
Properties & Relations (4)
MatrixExp applied to ![]() with
with ![]() sampled from GaussianUnitaryMatrixDistribution is unitary:
sampled from GaussianUnitaryMatrixDistribution is unitary:
Estimate the parameters of the distribution of elements of matrices drawn from GaussianUnitaryMatrixDistribution, assuming they are independent and normally distributed:
The spectral density of large GUE matrix converges to WignerSemicircleDistribution:
Compare the histogram with the PDF:
The distribution of scaled largest eigenvalue of large GUE matrices converges to TracyWidomDistribution:
Compare sample histogram with the PDF of TracyWidomDistribution[2]:
Related Guides
Text
Wolfram Research (2015), GaussianUnitaryMatrixDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/GaussianUnitaryMatrixDistribution.html (updated 2017).
CMS
Wolfram Language. 2015. "GaussianUnitaryMatrixDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/GaussianUnitaryMatrixDistribution.html.
APA
Wolfram Language. (2015). GaussianUnitaryMatrixDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GaussianUnitaryMatrixDistribution.html
BibTeX
@misc{reference.wolfram_2025_gaussianunitarymatrixdistribution, author="Wolfram Research", title="{GaussianUnitaryMatrixDistribution}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/GaussianUnitaryMatrixDistribution.html}", note=[Accessed: 01-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_gaussianunitarymatrixdistribution, organization={Wolfram Research}, title={GaussianUnitaryMatrixDistribution}, year={2017}, url={https://reference.wolfram.com/language/ref/GaussianUnitaryMatrixDistribution.html}, note=[Accessed: 01-March-2026]}