TracyWidomDistribution
Dyson指数が β のTracy–Widom分布を表す.
詳細
- Tracy–Widom分布は,ガウス型アンサンプルに属するランダム行列の正規化された最大固有値の極限確率分布である.
- TracyWidomDistributionでは,Dyson指数 β は,もとになっている行列分布によって,1,2または4である.
-
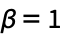
GaussianOrthogonalMatrixDistribution β2 GaussianUnitaryMatrixDistribution β4 GaussianSymplecticMatrixDistribution - TracyWidomDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
例題
すべて開くすべて閉じるスコープ (4)
アプリケーション (4)
MatrixPropertyDistributionを使ってガウス型ユニタリアンサンブルからの行列の正規化された最大固有値を表す:
MatrixPropertyDistributionからのサンプル:
ガウス型の直交アンサンブルとガウス型のシンプレクティックアンサンブルで同様の計算を行う:
n と p(共分散行列Σの次元)が両方とも大きい場合,恒等共分散を持つWishartアンサンブルからの行列のスケールされた最大固有値は,ほぼ ![]() のTracy–Widom分布として分布する:
のTracy–Widom分布として分布する:
スケールされた最大固有値のヒストグラムを確率密度関数と比較する:
Tracy–Widom分布の累積分布関数を対数スケールにおける左裾部上のリーディングオーダー漸近展開と比較する:
指定された数列におけるLongestOrderedSequenceの長さを求める関数を定義する:
特性と関係 (2)
β のさまざまな値についてのTracy–Widom分布の累積分布関数は互いに関係がある:
Tracy–Widom分布の中心部分はGammaDistributionでうまく近似することができる:
![]() のTracy–Widom分布とGammaDistributionを最初の3つのモーメントについてマッチする:
のTracy–Widom分布とGammaDistributionを最初の3つのモーメントについてマッチする:
テキスト
Wolfram Research (2015), TracyWidomDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/TracyWidomDistribution.html.
CMS
Wolfram Language. 2015. "TracyWidomDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TracyWidomDistribution.html.
APA
Wolfram Language. (2015). TracyWidomDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TracyWidomDistribution.html