Search for all pages containing Tuples


Tuples
Details
- The elements of list are treated as distinct, so that Tuples[list,n] for a list of length k gives output of length kn.
- Tuples[list,n] is equivalent to Tuples[Table[list,n]].
- The order of elements in Tuples[list,n] is based on the order of elements in list, so that Tuples[{a1,…,ak},n] gives
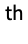 .
. - The object list need not have head List. The head at each level in the arrays generated by Tuples will be the same as the head of list.
Examples
open all close allBasic Examples (3)
Generalizations & Extensions (3)
Applications (8)
Properties & Relations (4)
Possible Issues (1)
See Also
Outer Array IntegerDigits Permutations Subsets Groupings Distribute
Function Repository: StringTuples SelectTuples TupleFromIndex TupleIndex OrderedTupleFromIndex OrderedTupleIndex
Tech Notes
Related Guides
History
Introduced in 2004 (5.1)
Text
Wolfram Research (2004), Tuples, Wolfram Language function, https://reference.wolfram.com/language/ref/Tuples.html.
CMS
Wolfram Language. 2004. "Tuples." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Tuples.html.
APA
Wolfram Language. (2004). Tuples. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Tuples.html
BibTeX
@misc{reference.wolfram_2025_tuples, author="Wolfram Research", title="{Tuples}", year="2004", howpublished="\url{https://reference.wolfram.com/language/ref/Tuples.html}", note=[Accessed: 05-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_tuples, organization={Wolfram Research}, title={Tuples}, year={2004}, url={https://reference.wolfram.com/language/ref/Tuples.html}, note=[Accessed: 05-February-2026]}