UnitRootTest

UnitRootTest[data]

データが単位根を持つ自己回帰時系列過程からのものかどうかの検定を行う．

UnitRootTest[data,model,"property"]

指定されたモデルに対する"property"の値を返す．

詳細とオプション

  • UnitRootTestは，時系列 data について，ARモデルを満たす時系列が対応する伝達関数の分母に単位根を持つという帰無仮説 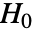とそうではないという対立仮説 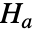で仮定検定を行う．
  • 帰無仮説の棄却で，トレンドを除去された data が定常時系列からのものである可能性がある，という結論が可能になる．
  • デフォルトで，確率値つまり 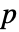値が返される．
  • 小さい 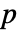値は単位根の存在可能性が低いことを示す．
  • data は値のリスト{x1,x2,…,xn}あるいはTemporalDataオブジェクトである．
  • model にはモデル 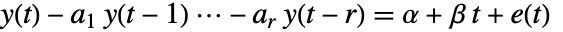の指定が可能である．ただし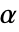， は一定のオフセット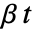， は線形ドリフト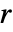， はARモデルの次数である．
  • 次の model 指定を使うことができる．
  • Automatic 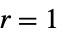かつ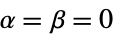
    r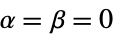
    "Constant" 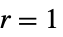かつ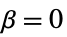
    "Drift"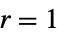
    {"Constant",r}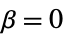
    {"Drift", r}一般的なケース
  • UnitRootTest[data]は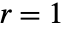，と 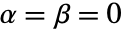でDickey–Fuller F検定を選択する．
  • UnitRootTest[data,model,All]は data と model に適用されるすべての検定を選択する．
  • UnitRootTest[data,model,"test"]は"test"による 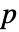値を報告する．
  • 使用可能な検定
  • "DickeyFullerF"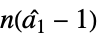に基づく
    "DickeyFullerT"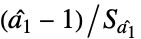に基づく
    "PhillipsPerronF"補正Dickey–Fuller F検定
    "PhillipsPerronT"補正Dickey–Fuller T検定
  • UnitRootTest[data,model,"HypothesisTestData"]は，htd["property"]の形で追加的な検定結果と特性の抽出に使うことができるHypothesisTestDataオブジェクト htd を返す．
  • UnitRootTest[data,model,"property"]を使って直接"property"の値を与えることができる．
  • 検定結果のレポートに関連する特性
  • "AllTests"適用可能な検定すべてのリスト
    "AutomaticTest"Automaticが使われた場合に選ばれる検定
    "PValue" 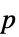値のリスト
    "PValueTable" 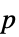値のフォーマットされた表
    "ShortTestConclusion"検定結果の簡単な説明
    "TestConclusion"検定結果の説明
    "TestData"検定統計と 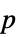値のペアのリスト
    "TestDataTable"検定統計と 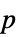値のフォーマットされた表
    "TestStatistic"検定統計のリスト
    "TestStatisticTable"検定統計のフォーマットされた表
  • 使用可能なオプション
  • SignificanceLevel 0.05診断とレポートのための切捨て
  • 単位根検定では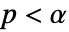， のときにのみ 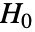が棄却されるような切捨て 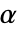が選択される．特性"TestConclusion"および"ShortTestConclusion"で使われる 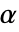の値はSignificanceLevelオプションで制御される．デフォルトで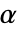， は0.05に設定されている．

例題

すべて開くすべて閉じる

例  (1)

時系列に単位根があるかどうかの検定を行う：

このデータは弱定常過程からのものである：

スコープ  (17)

検定  (13)

時系列データを単位根について検定する：

単位根が存在する場合， 値は一般に大きくなる：

単位根が存在しない場合， 値は一般に小さくなる：

もとになっているモデルがARProcess[2]であるという帰無仮説での単位根の検定：

モデルをAutomaticに設定することは，もとになるARProcess[1]を仮定することに等しい：

もとになる非零の平均を説明する単位根についての検定を行う：

非零の平均を説明し，もとになるARProcess[3]を仮定する：

非零の平均と確定的トレンドを仮定する：

非零平均，確定的トレンド，もとになっているARProcess[3]を仮定する：

単位根について特定の検定を行う：

任意数の検定を同時に行うことが出できる：

Automaticを使うとDickey–Fuller F検定が適用される：

特性"AutomaticTest"を使ってどの検定が選ばれたのかを知ることができる：

データに適したすべての検定を同時に行う：

特性"AllTests"を使ってどの検定が使われたのかを特定する：

繰り返し特性を抽出するためにHypothesisTestDataオブジェクトを作る：

抽出可能な特性：

HypothesisTestDataオブジェクトからいくつかの特性を抽出する：

"DickeyFullerT"検定からの 値と検定統計：

任意数の特性を同時に抽出する：

Dickey–Fuller F検定からの 値と検定統計：

レポート  (4)

選択した検定からの結果を表にする：

適切なすべての検定結果の完全な表：

選択された検定結果の表：

カスタムレポートのために検定表から項目を取り出す：

値は0.05より大きいので，このレベルでは を棄却するための十分な証拠はない：

検定あるいは検定集合のために 値を表にする：

表からの 値：

適切なすべての検定からの 値の表：

検定の部分集合からの 値の表：

検定あるいは検定集合からの検定統計を報告する：

表からの検定統計：

適切なすべての検定からの検定統計の表：

オプション  (1)

SignificanceLevel  (1)

有意水準は"TestConclusion"と"ShortTestConclusion"に用いられる：

アプリケーション  (3)

オーストラリアのシドニーの47年間に渡る1日あたりの最大降雨量が記録されている．単純な自己回帰モデルでこのデータがモデル化できるだろうか：

このデータには明らかに非零平均がある：

Schwertの経験則を使ってもとになっているARProcessの次数を選ぶ：

単位根があるということは，単純なARProcessが適切なモデルではないことを示唆する：

1937年から1960年までのアメリカ合衆国の民間航空会社の年間収入（単位：百万ドル）について考える：

トレンドはUnitRootTestを使って確認できる：

線形トレンドを除くだけで十分なように見える：

ARIMAProcessを時系列にフィットする：

フィットされたモデルを使って，その後10年の収入を予測する：

SP500指標の予測：

単位根検定を使ってトレンドの存在を確かめる：

非零の和分次数のARIMAをフィットする：

翌月の予測を求める：

考えられる問題  (2)

Phillips–Perron検定はARProcess[1]モデルに限られている：

より高次にはDickey–Fullerタイプの検定を使う：

UnitRootTestは，不等間隔データではうまくいかない：

値のみを使う：

あるいは，TemporalRegularityを真に設定する：

おもしろい例題  (2)

サンプルサイズ100でDickey–Fuller T分布の近似のシミュレーションを行う：

最初のシミュレーションのデータ集合の検定統計と 値：

シミュレーションによる分布を使うと，同じような結果が返される：

帰無仮説のもとでのある検定統計の近似分布：

Wolfram Research (2012), UnitRootTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/UnitRootTest.html.

テキスト

Wolfram Research (2012), UnitRootTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/UnitRootTest.html.

CMS

Wolfram Language. 2012. "UnitRootTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/UnitRootTest.html.

APA

Wolfram Language. (2012). UnitRootTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/UnitRootTest.html

BibTeX

@misc{reference.wolfram_2024_unitroottest, author="Wolfram Research", title="{UnitRootTest}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/UnitRootTest.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_unitroottest, organization={Wolfram Research}, title={UnitRootTest}, year={2012}, url={https://reference.wolfram.com/language/ref/UnitRootTest.html}, note=[Accessed: 21-November-2024 ]}