WilksW
WilksW[m1,m2]
对于矩阵 m1 和 m2 给出 Wilks 的 .
更多信息
- WilksW[m1,m2] 给出介于 m1 和 m2 之间的 Wilks 的 .
- Wilks 的 是基于合并的协方差矩阵的分区的线性相关的一个测量.
- Wilks 的 被计算为
![1-TemplateBox[{Sigma}, Det]/(TemplateBox[{{Sigma, _, {(, 11, )}}}, Det] TemplateBox[{{Sigma, _, {(, 22, )}}}, Det]) 1-TemplateBox[{Sigma}, Det]/(TemplateBox[{{Sigma, _, {(, 11, )}}}, Det] TemplateBox[{{Sigma, _, {(, 22, )}}}, Det])](Files/WilksW.zh/1.png) ,其中
,其中 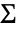 是合并样本的协方差矩阵,可以分成
是合并样本的协方差矩阵,可以分成  ,其中
,其中 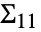 和
和  对应于单个数据集的协方差矩阵.
对应于单个数据集的协方差矩阵. - 参变量 m1 和 m2 可以是具有同等长度的任何实数值矩阵或向量.
范例
打开所有单元关闭所有单元属性和关系 (3)
Wolfram Research (2012),WilksW,Wolfram 语言函数,https://reference.wolfram.com/language/ref/WilksW.html.
文本
Wolfram Research (2012),WilksW,Wolfram 语言函数,https://reference.wolfram.com/language/ref/WilksW.html.
CMS
Wolfram 语言. 2012. "WilksW." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/WilksW.html.
APA
Wolfram 语言. (2012). WilksW. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/WilksW.html 年