-
See Also
- TreeGraph
- Graph
- CreateDataStructure
- DataStructure
-
- Data Structures
- RedBlackTree
- AVLTree
- Related Guides
"BinaryTree" (Data Structure)
"BinaryTree"
represents a mutable binary tree where the values stored at each node are general expressions.
Details


- A binary tree is useful for accessing nodes based on data associated with each node as well as for representing hierarchical relationships with up to two branches:
-
CreateDataStructure["BinaryTree",v] create a new "BinaryTree" with specified initial value v and empty left and right children CreateDataStructure["BinaryTree",v{l,r}] create a new "BinaryTree" with specified initial value v and specified left and right children Typed[x,"BinaryTree"] give x the type "BinaryTree" - For a data structure of type "BinaryTree", the following operations can be used:
-
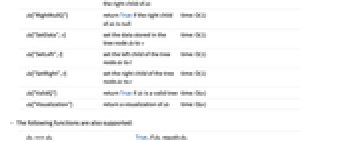
ds["BreadthFirstScan",f] perform a breadth-first scan of ds, passing the data in each node to f time: O(n) ds["Copy"] return a copy of ds time: O(n) ds["Data"] return the data stored in the tree node ds time: O(1) ds["InOrderScan",f] perform an in-order scan of ds, passing the data in each node to f time: O(n) ds["Left"] return the data structure for the left child of ds time: O(1) ds["LeftNullQ"] return True if the left child of ds is null time: O(1) ds["NullQ"] return True if ds is null time: O(1) ds["PostOrderScan",f] perform a post-order scan of ds, passing the data in each node to f time: O(n) ds["PreOrderScan",f] perform a pre-order scan of ds, passing the data in each node to f time: O(n) ds["Right"] return the data structure for the right child of ds time: O(1) ds["RightNullQ"] return True if the right child of ds is null time: O(1) ds["SetData",v] set the data stored in the tree node ds to v time: O(1) ds["SetLeft",l] set the left child of the tree node ds to l time: O(1) ds["SetRight",r] set the right child of the tree node ds to r time: O(1) ds["ValidQ"] return True if ds is a valid tree time: O(n) ds["Visualization"] return a visualization of ds time: O(n) - The following functions are also supported:
-
dsi===dsj True, if dsi equals dsj FullForm[ds] the full form of ds Information[ds] information about ds InputForm[ds] the input form of ds Normal[ds] convert ds to a normal expression
Examples
open all close allBasic Examples (2)
A new "BinaryTree" can be created with CreateDataStructure:
Insert a new value to be stored:
Confirm that the value has updated:
Create a new "BinaryTree" with specified children:
Scope (1)
Information (1)
A new "BinaryTree" can be created with CreateDataStructure:
Applications (7)
Binary Search Tree (1)
One use of a binary tree is for storing ordered material. Typically these are called binary search trees. Here is a simple insertion program:
Create a binary tree and insert 30 random numbers:
This makes an in-order scan over the binary tree. Since it is sorted, the elements are visited in sorted order, as shown in this example:
A problem with a basic binary search tree like this is that the insertion chains can become unbalanced, so that the maximum depth of the tree becomes large. This problem is corrected by the various forms of balanced binary trees.
Tree Rotation (1)
Tree rotation on a sorted binary tree involves a change to the structure of the tree while maintaining the order of elements. Rotations are used by many techniques for creating balanced binary trees.
Some basic tree rotation operations for right and left rotations are shown here:
A binary tree is created here. Note that it has two levels of nodes on the left and none on the right. This is an inefficient storage:
The right rotation moves the nodes to the right, maintaining the sorted property and making a more balanced tree:
The left rotation moves the nodes back to the left, also maintaining the sorted property:
Compute the Maximum Depth of a Binary Tree (1)
Find the Lowest Common Ancestor (1)
The lowest common ancestor of two nodes in a tree is the lowest (or deepest) node that has both nodes as a descendant. It can be computed with some simple code.
A program to insert random nodes into a tree. This uses a counter to make sure that all nodes are distinct:
Set the random seed to get a reproducible example:
Create a random tree and visualize it:
A program to find the lowest common ancestor:
Test if a Binary Tree is Symmetric (1)
Find the Diameter of a Binary Tree (1)
Possible Issues (2)
Null Nodes (1)
Create a binary tree with some data:
It is an error to carry out operations that work on the contents of a null node:
The serialization of a null node is Null:
Create a null node with CreateDataStructure:
A Wolfram Language representation of a null node is very useful, since it allows algorithms to be written that manipulate the nodes of a binary tree without having to check if they are null.
Valid Trees (1)
The Wolfram Language interface to binary trees is designed to be flexible and efficient. This has some consequences for the structures created.
Create a binary tree with some data:
Create another tree and make it the right child:
Now there is nothing in the operations that prevents making the right child equal to the parent:
The result is no longer a tree. This can be confirmed by using the "ValidQ" operation:
Some operations give errors if the tree is not valid:
The insertion functions do not give errors when an invalid structure is created because this would make them less efficient. Operations such as those that serialize the data structure have a built-in check.
Related Guides
History
Introduced in 2020 (12.1)