"Deque" (Data Structure)

"Deque"

represents a queue of expressions that can be added or removed from the front and back.

Details

  • A deque is a collection of elements that supports both first-in, first-out and last-in, first-out insertion and removal:
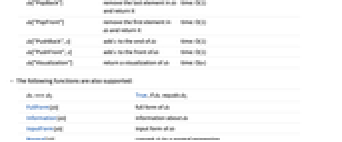
  • CreateDataStructure["Deque"]create a new empty "Deque"
    CreateDataStructure["Deque",elems]create a new "Deque" containing elems
    Typed[x,"Deque"]give x the type "Deque"
  • For a data structure of type "Deque", the following operations can be used:
  • ds["Copy"]return a copy of dstime: O(n)
    ds["DropAll"]drop all the elements from dstime: O(n)
    ds["Elements"]return a list of the elements of dstime: O(n)
    ds["EmptyQ"]True, if the ds is emptytime: O(1)
    ds["Fold",fun,init]apply fun to the elements of ds, starting with init, accumulating a resulttime: O(n)
    ds["Length"]number of elements in dstime: O(1)
    ds["PeekBack"]the last element in dstime: O(1)
    ds["PeekFront"]the first element in dstime: O(1)
    ds["PopBack"]remove the last element in ds and return ittime: O(1)
    ds["PopFront"]remove the first element in ds and return ittime: O(1)
    ds["PushBack",x]add x to the end of dstime: O(1)
    ds["PushBackList",elems]add elems to the end of dstime: O(nelems)
    ds["PushFront",x]add x to the front of dstime: O(1)
    ds["PushFrontList",elems]add elems to the front of dstime: O(nelems)
    ds["Visualization"]return a visualization of dstime: O(n)
  • The following functions are also supported:
  • dsi===dsjTrue, if dsi equals dsj
    FullForm[ds]full form of ds
    Information[ds]information about ds
    InputForm[ds]input form of ds
    Normal[ds]convert ds to a normal expression

Examples

open allclose all

Basic Examples  (2)

A new "Deque" can be created with CreateDataStructure:

ds is initially empty:

Add an element to ds:

ds is no longer empty:

It has one element:

Add another element and peek. This shows the first element:

Remove the last element and return it:

Return an expression version of ds:

It is fast to put elements into a queue:

A visualization of the data structure can be generated:

Sum all the elements:

Scope  (1)

Information  (1)

A new "Deque" can be created with CreateDataStructure:

Information about the data structure ds:

Applications  (1)

Minimum of a Partially Ordered Set  (1)

A "Deque" is useful for computing the minimum of a partially ordered set. A partially ordered set needs an ordering function that can return Indeterminate if the elements do not have an ordering relation.

This returns the minimum of a set for the ordering function or Indeterminate if there is no minimum value:

This ordering function uses Divisible; if the numbers are not divisible by each other, the result is Indeterminate:

2 can be divided into both 4 and 6, so it is the minimum value:

There is no number here that can be divided into the others; the result is Indeterminate: