"RedBlackTree" (データ構造)

"RedBlackTree"

各ノードにおいて保存される値が一般式である可変平衡二分探索木を表す．

詳細

  • 二分探索木は，挿入操作が素早くできる整理された形式でデータを保存する．平衡二分探索木では，すべての枝の高さが必ず平衡である．これによって，任意の挿入や削除にも関わらず，操作が効率的であるようにすることができる．
  • CreateDataStructure[ "RedBlackTree"]新しい空の"RedBlackTree"を作成する
    CreateDataStructure["RedBlackTree",v{l,r}]指定の初期値 v と指定の左と右の子を持つ新しい"RedBlackTree"を作成する
    CreateDataStructure["RedBlackTree",tree,p]指定の木と順序関数 p を持つ新しい"RedBlackTree"を作成する
    Typed[x,"RedBlackTree"]x に "RedBlackTree"型を与える
  • "RedBlackTree"型のデータ構造には，以下の演算が使える．
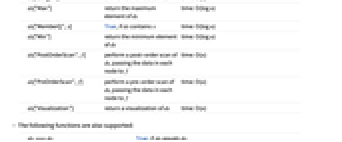
  • ds["BreadthFirstScan",f]ds の幅優先探索を行い，各ノードのデータを f に渡すtime: O(n)
    ds["Copy"]ds のコピーを返すtime: O(n)
    ds["Delete",x]x を ds から削除するtime: O(log n)
    ds["DeleteAll"]ds からすべての要素を削除するtime: O(n)
    ds["DropMax"]ds の最大要素を取り除き，それを返すtime: O(log n)
    ds["DropMin"]ds の最小要素を取り除き，それを返すtime: O(log n)
    ds["Elements"]ds の要素のリストを返すtime: O(n)
    ds["EmptyQ"]ds がノードを持たない場合はTruetime: O(1)
    ds["FreeQ",x]ds が x を含まない場合はTruetime: O(log n)
    ds["InOrderScan",f]ds の間順探索を行い，各ノードのデータを f に渡すtime: O(n)
    ds["Insert",x]x を ds に挿入するtime: O(log n)
    ds["Length"]ds のノードの数time: O(1)
    ds["Max"]ds の最大要素を返すtime: O(log n)
    ds["MemberQ",x]ds が x を含む場合はTruetime: O(log n)
    ds["Min"]ds の最小要素を返すtime: O(log n)
    ds["PostOrderScan",f]ds の後順探索を行い，各ノードのデータを f に渡すtime: O(n)
    ds["PreOrderScan",f]ds の前順探索を行い，各ノードのデータを f に渡すtime: O(n)
    ds["Visualization"]ds の可視化を返すtime: O(n)
  • 以下の関数もサポートする．
  • dsi===dsjdsi が dsj に等しい場合はTrue
    FullForm[ds]ds の完全形
    Information[ds]ds についての情報
    InputForm[ds]ds の入力形
    Normal[ds]ds を通常の式に変換する
  • 2つの要素の順序は，Sortの順序関数によって与えられる解釈に従い，順序関数 p によって決定される．デフォルトの順序関数は，Orderである．
  • "RedBlackTree"は，各部分木の高さが決して2以上異なることがないように，平衡特性を維持する．
  • 最初の木の指定がNullである場合には，空の"RedBlackTree"が作成される．

例題

すべて開くすべて閉じる

例  (1)

新しい"RedBlackTree"は，CreateDataStructureを使って作成できる：

複数の値を挿入する：

データ構造の可視化を生成することができる：

スコープ  (4)

情報  (1)

新しい"RedBlackTree"は，CreateDataStructureを使って作成することができる：

データ構造 ds についての情報：

平衡  (1)

"RedBlackTree"は，色付けの特性（通常，赤か黒で表示される）を使って平衡を保つ：

平衡特性を崩す変更を行うと，再度平衡になるように調整される：

これで右に挿入しても再度平衡を取る必要はない：

左から削除すると，再度平衡にする必要がある：

順序  (1)

新しい木を作成し，30個の乱数を挿入する：

木に対して間順探索が行われる．ソートされるので，この例が示すように，ソートされた順に要素を訪れる：

順序関数  (1)

カスタム順序関数で空の木を作成する：

データを挿入する：

木の要素：

最大要素を削除して返す：

最大要素は削除された：