"LLE" (機械学習メソッド)

詳細とサブオプション

  • "LLE"は，局所線形埋込みを表す，非線形近傍保存次元性削減メソッドである．
  • "LLE"は非線形多様体を学ぶことができるが，データに高密度の変動がある場合では失敗することがあり，データの大部分が互いに接近している場合は崩壊する傾向がある．
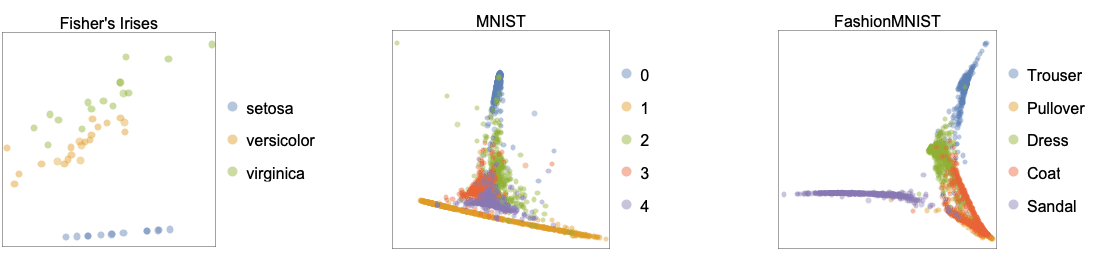
  • 次のプロット（FeatureSpacePlotを参照のこと）は，"LLE"メソッドが学習した二次元埋込みを，Fisher's Irises，MNIST，FashionMNISTのベンチマークデータ集合に適用した結果を示している．
  • "LLE"は，データ固有の幾何特性（角度や相対距離等）を局所的に保持する低次元の埋込みを見付けようとする．そのために，"LLE"は，まず，各データ点の近傍をその 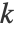最近傍で定義する．次に，最適な「再構築の重み」Wijを，再構築誤差を最小にすることで計算する（xjは xiの近傍）． ∑ Ni=1|xi-∑jWijxj|2 これは制約条件 ∑jWij=1に従う．この制約条件は，データの回転，リスケーリング，平行移動に対する Wijの不変性を強制する．Wijが計算されると，埋め込みコストを最小にすることで低次元埋込み 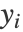が計算される．∑ Ni=1|yi-∑jWijyj|2
  • "LLE"は，もとの空間と削減空間の両方で同じ再構築の重みを持たせようとする．このためデータ点の局所幾何特性がほぼ保存される．
  • 次は，使用可能なサブオプションである．
  • "NeighborsNumber" Automatic最近傍 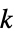の数

例題

すべて開くすべて閉じる

例  (1)

「スイスロール」データ集合を作成して可視化する：

"LLE"をデータ集合に使って二次元空間にマッピングすることで非線形次元削減器を訓練する：

削減空間でデータの座標を求めて可視化する：

データ集合をもとの空間で，各点をその削減した変数によって彩色して，可視化する：

スコープ  (1)

データ集合の可視化  (1)

ExampleDataからFisherのアヤメに関するデータ集合をロードして，訓練集合と検定集合に分割する：

"LLE"で削減関数を各訓練例の特徴とともに生成する：

検定例をその種によってグループ化する：

特徴の次元を削減する：

削減したデータ集合を可視化する：

オプション  (1)

"NeighborsNumber"  (1)

3D幾何データから，ランダムな視点によるさまざまな頭部の向きのデータ集合を生成する：

さまざまな頭部の向きを可視化する：

局所線形埋込みを行うために，近傍グラフで"NeighborsNumber"を指定することで，データ集合を二次元表現に削減する：

上下と前横の向きのもつれが解消された削減空間でもとの画像を可視化する：