"Linear" (Machine Learning Method)
- Method for DimensionReduction, DimensionReduce, FeatureSpacePlot and FeatureSpacePlot3D.
- Maps the data into a linear lower-dimensional space.
Details & Suboptions
- "Linear" is a linear dimensionality reduction method. The method learns a low-dimensional representation of data via a linear mapping.
- "Linear" works for datasets that have a large number of features, large number of examples and possibly many missing values (and hence can be used for collaborative filtering); however it can fail for datasets with nonlinear manifolds.
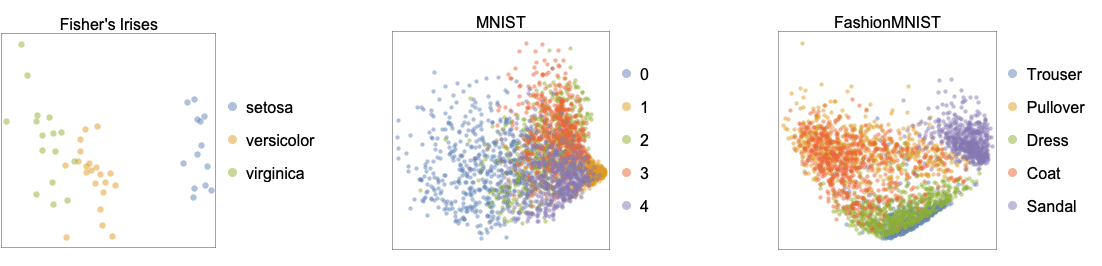
- The following plots show the results of the "Linear" method applied to benchmark datasets Fisher's Irises, MNIST and FashionMNIST:
- Depending on the data, the "Linear" method either first standardizes the data (it effectively becomes the "PrincipalComponentsAnalysis" method) or keeps the data as is (it effectively becomes the "LatentSemanticAnalysis" method).
- Learned parameters are a matrix of size
 where
where 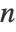 and
and  are the original and final dimensions of the data. The reduction is done through a matrix multiplication.
are the original and final dimensions of the data. The reduction is done through a matrix multiplication. - Parameters are found by minimizing the reconstruction error (mean squared error) of the training data.
- Internally, procedures like singular value decomposition, alternating least squares and power iteration are used.
Examples
open all close allBasic Examples (1)
Scope (1)
Dataset Visualization (1)
Load the Fisher Iris dataset from ExampleData:
Generate a reducer function using "Linear" with the features of each example:
Group the examples by their species: