"LLE" （机器学习方法）

详细信息和子选项

  • "LLE" 代表局部线性嵌入，是一种非线性的邻域保留降维方法.
  • "LLE" 能够学习非线性流形； 但如果数据具有高密度变化，则可能会失败，并且倾向于将大部分数据折叠在一起.
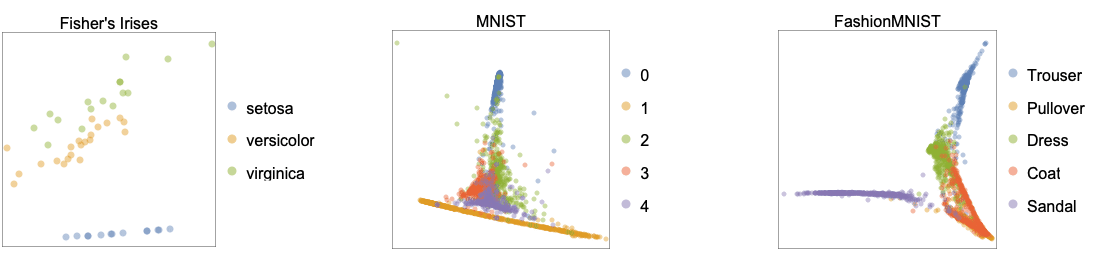
  • 下图（参阅 FeatureSpacePlot）显示了应用于基准数据集 Fisher's Irises、MNIST 和 FashionMNIST 的 "LLE" 方法学习的二维嵌入：
  • "LLE" 寻求找到一种低维嵌入，局部保留数据的固有几何形状（例如角度和相对距离）. 为此，"LLE" 首先通过其 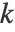个最近邻定义每个数据点的邻域. 然后，它通过最小化重构误差（xj 是 xi 的近邻）来计算最佳“重构权重” Wij： ∑ Ni=1|xi-∑jWijxj|2，受制于约束 ∑jWij=1（此约束强制 Wij 对数据的旋转、重新缩放和平移具有不变性）. 一旦计算出 Wij，低维嵌入 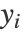就可以通过最小化嵌入成本来计算得到：                      ∑ Ni=1|yi-∑jWijyj|2.
  • "LLE" 试图在原始空间和嵌入空间中具有相同的重构权重，这正是数据点的局部几何属性得以保留的原因.
  • 可以给出以下子选项：
  • "NeighborsNumber" Automatic最近邻数量

范例

打开所有单元关闭所有单元

基本范例  (1)

创建并可视化“瑞士卷”数据集：

在数据集上使用 "LLE" 训练非线性降维函数以映射到二维空间：

查找并可视化降维后空间中的数据坐标：

在原始空间中可视化数据集，每个点根据其降维的变量着色：

范围  (1)

数据集可视化  (1)

从 ExampleData 加载 Fisher Iris 数据集并执行训练/测试拆分：

使用 "LLE" 生成具有每个训练示例特征的降维函数：

按物种对示例进行分组：

降低特征的维度：

可视化降维后的数据集：

选项  (1)

"NeighborsNumber"  (1)

从具有随机视点的三维几何数据生成不同头部姿势的数据集：

可视化不同的头部姿势：

通过在邻域图中指定 "NeighborsNumber" 来执行局部线性嵌入，将数据集简化为二维表示：

在降维后的空间中可视化原始图像，其中上下和正侧面姿势被拆解：