"LinearRegression" (Machine Learning Method)

Details & Suboptions

  • The linear regression predicts the numerical output y using a linear combination of numerical features 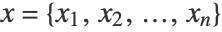. The conditional probability 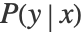is modeled according to 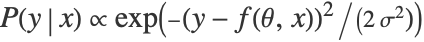, with .
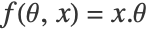  • The estimation of the parameter vector θ is done by minimizing the loss function 1/2sum_(i=1)^m(y_i-f(theta,x_i))^2+lambda_1sum_(i=1)^nTemplateBox[{{theta, _, i}}, Abs]+(lambda_2)/2 sum_(i=1)^ntheta_i^2, where m is the number of examples and n is the number of numerical features.
  • The following suboptions can be given:
  • "L1Regularization" 0value of 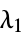in the loss function
    "L2Regularization" Automaticvalue of 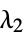iin the loss function
    "OptimizationMethod" Automaticwhat optimization method to use
  • Possible settings for the "OptimizationMethod" option include:
  • "NormalEquation"linear algebra method
    "StochasticGradientDescent"stochastic gradient method
    "OrthantWiseQuasiNewton"orthant-wise quasi-Newton method
  • For this method, Information[PredictorFunction[…],"Function"] gives a simple expression to compute the predicted value from the features.

Examples

open allclose all

Basic Examples  (2)

Train a predictor on labeled examples:

Look at the Information:

Predict a new example:

Generate two-dimensional data:

Train a predictor function on it:

Compare the data with the predicted values and look at the standard deviation:

Options  (5)

"L1Regularization"  (2)

Use the "L1Regularization" option to train a predictor:

Generate a training set and visualize it:

Train two predictors by using different values of the "L1Regularization" option:

Look at the predictor function to see how the larger L1 regularization has forced one parameter to be zero:

"L2Regularization"  (2)

Use the "L2Regularization" option to train a predictor:

Generate a training set and visualize it:

Train two predictors by using different values of the "L2Regularization" option:

Look at the predictor functions to see how the L2 regularization has reduced the norm of the parameter vector:

"OptimizationMethod"  (1)

Generate a large training set:

Train predictors with different optimization methods and compare their training times: