"LinearRegression" (机器学习方法)
- Predict 的方法.
- 使用特征的线性组合预测值.
详细信息与子选项
- 使用数值特征
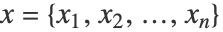 的线性组合,线性回归预测数值输出 y. 条件概率
的线性组合,线性回归预测数值输出 y. 条件概率  根据
根据 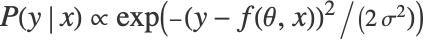 ,其中
,其中 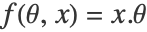 被模拟.
被模拟. - 参数向量 θ 的估计是根据最小化损失函数
![1/2sum_(i=1)^m(y_i-f(theta,x_i))^2+lambda_1sum_(i=1)^nTemplateBox[{{theta, _, i}}, Abs]+(lambda_2)/2 sum_(i=1)^ntheta_i^2 1/2sum_(i=1)^m(y_i-f(theta,x_i))^2+lambda_1sum_(i=1)^nTemplateBox[{{theta, _, i}}, Abs]+(lambda_2)/2 sum_(i=1)^ntheta_i^2](Files/LinearRegression.zh/5.png) 得到,其中,m 是例子数,n 是数值特征数.
得到,其中,m 是例子数,n 是数值特征数. - 可以给出以下子选项:
-
"L1Regularization" 0 损失函数中的 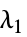 值
值"L2Regularization" Automatic 损失函数中的 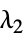 值
值"OptimizationMethod" Automatic 使用何种优化方法 - "OptimizationMethod" 选项的可能设置是:
-
"NormalEquation" 线性代数方法 "StochasticGradientDescent" 随机梯度方法 "OrthantWiseQuasiNewton" orthant-wise quasi-Newton 方法 - 对于这种方法,Information[PredictorFunction[…],"Function"] 给出简单的表达式根据特征计算预测值.
范例
打开所有单元关闭所有单元基本范例 (2)常见实例总结
In[1]:=1
✖
https://wolfram.com/xid/0bqb5x3dcmnm-wxc5bs
Out[1]=1
查看 Information:
In[2]:=2
✖
https://wolfram.com/xid/0bqb5x3dcmnm-3656v8
Out[2]=2
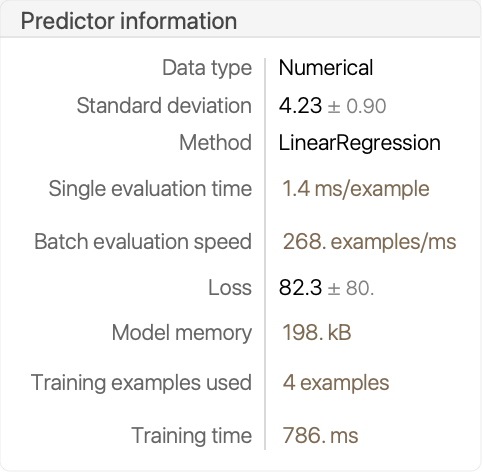
In[3]:=3
✖
https://wolfram.com/xid/0bqb5x3dcmnm-tgze8s
Out[3]=3
In[1]:=1

✖
https://wolfram.com/xid/0bqb5x3dcmnm-ef76x2
Out[1]=1
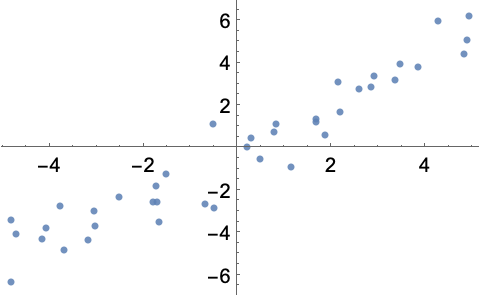
In[2]:=2
✖
https://wolfram.com/xid/0bqb5x3dcmnm-fj7crm
Out[2]=2
In[3]:=3

✖
https://wolfram.com/xid/0bqb5x3dcmnm-bcq515
Out[3]=3
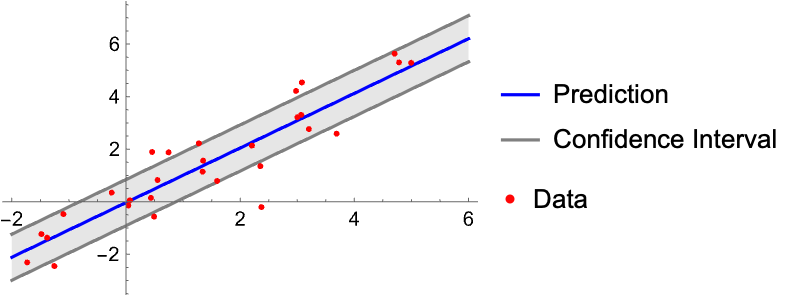
选项 (5)各选项的常用值和功能
"L1Regularization" (2)
使用 "L1Regularization" 选项培训预测器:
In[1]:=1
✖
https://wolfram.com/xid/0bqb5x3dcmnm-8d3hj3
Out[1]=1
In[1]:=1
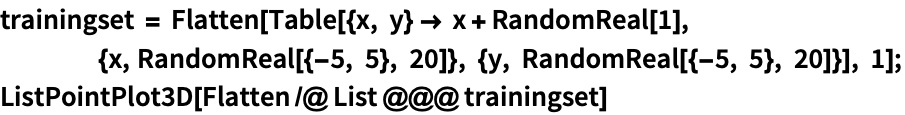
✖
https://wolfram.com/xid/0bqb5x3dcmnm-z6fnrr
Out[1]=1
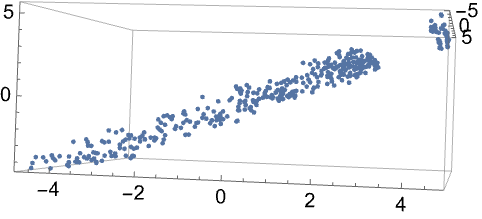
通过使用 "L1Regularization" 选项的不同值培训两个预测器:
In[2]:=2
✖
https://wolfram.com/xid/0bqb5x3dcmnm-qm6f1x
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bqb5x3dcmnm-718tom
Out[3]=3
查看预测器函数,看多大的 L1 正则化已经强制一个参数为 0:
In[4]:=4
✖
https://wolfram.com/xid/0bqb5x3dcmnm-hs69mo
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0bqb5x3dcmnm-psj2uv
Out[5]=5
"L2Regularization" (2)
使用 "L2Regularization" 选项培训预测器:
In[1]:=1
✖
https://wolfram.com/xid/0bqb5x3dcmnm-zbcx6b
Out[1]=1
In[1]:=1
✖
https://wolfram.com/xid/0bqb5x3dcmnm-zfni0z
Out[1]=1
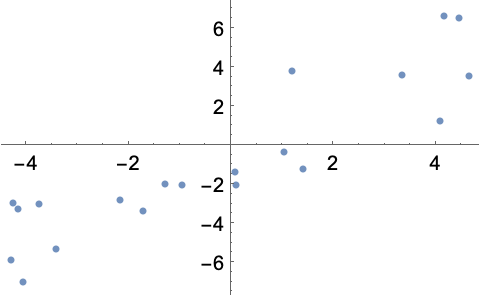
通过使用 "L2Regularization" 选项的不同值培训两个预测器:
In[2]:=2
✖
https://wolfram.com/xid/0bqb5x3dcmnm-6md8tb
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bqb5x3dcmnm-z9k0eu
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0bqb5x3dcmnm-8l4sma
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0bqb5x3dcmnm-chnthl
Out[5]=5