"MultidimensionalScaling" （机器学习方法）

Details & Suboptions

  • "MultidimensionalScaling" 是一种基于距离的非线性降维方法. 该方法试图通过保持数据点之间的成对距离来找到数据的低维嵌入.
  • "MultidimensionalScaling" 能够学习非线性流形；然而，当样本数量很大时，它可能会变得较慢.
  • 以下图表展示了 "MultidimensionalScaling" 方法应用于基准数据集 Fisher's Irises、MNIST 和 FashionMNIST 后学习到的二维嵌入：
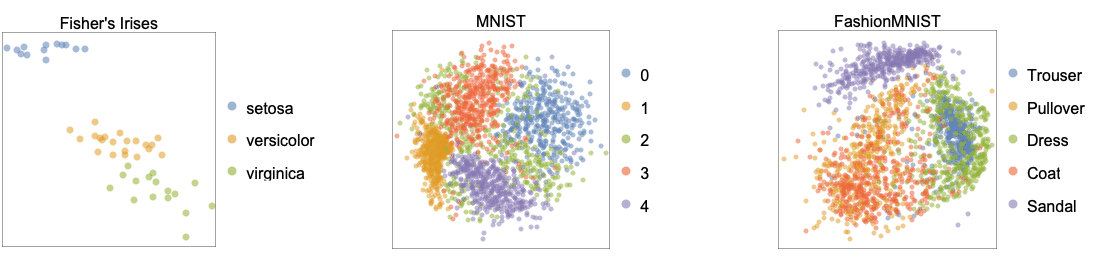
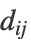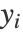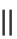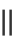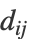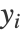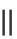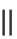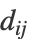  • 给定原始空间中数据点的距离矩阵 d_(ij)，"MultidimensionalScaling" 试图找到低维嵌入 ，使得在低维空间中的距离与原始空间中数据点之间的距离相匹配，即||yi-yj||≈ d_(ij). 低维嵌入 通过最小化以下嵌入成本来计算： ∑i,j [||yi-yj||- d_(ij)]2.
  • 可以给出以下子选项：
  • MaxIterations Automatic优化步骤的最大次数
    "MinRelativeChange"Automatic成本值的最小相对变化，以继续优化过程

范例

打开所有单元关闭所有单元

基本范例  (2)

使用 "MultidimensionalScaling" 方法降低随机向量的维数：

创建并可视化“瑞士卷”数据集：

在数据集上使用 "MultidimensionalScaling" 训练非线性降维器以映射到二维空间：

在降维的空间中查找并可视化数据坐标：

在原始空间中可视化数据集，每个点根据其减少的变量着色：

范围  (1)

数据集可视化  (1)

从 ExampleData 加载 Fisher Iris 数据集：

使用 "MultidimensionalScaling" 根据每个示例的特征生成一个降维函数：

根据物种对示例进行分组：

降低特征的维度：

可视化降维后的数据集：

选项  (1)

MaxIterations  (1)

加载 "MNIST" 数据集：

使用 "MultidimensionalScaling" 降低图像的维度：

使用不同的 MaxIterations 选项查找降维后的特征：

将获得的特征可视化，并比较结果：