"TSNE" (Machine Learning Method)
- Method for DimensionReduction, DimensionReduce, FeatureSpacePlot and FeatureSpacePlot3D.
- Reduce the dimension of data using t-distributed stochastic neighbor embedding.
Details & Suboptions
- "TSNE", which stands for t-distributed stochastic neighbor embedding, is a nonlinear non-parametric dimensionality reduction method. The method attempts to learn a low-dimensional representation of the data that preserves the local structure of the data.
- "TSNE" works for datasets with nonlinear manifolds and is particularly suited for the visualization of high-dimensional datasets; however, it is slow to train for datasets that have a large number of features and large number of examples.
- The following shows two-dimensional embeddings learned by the "TSNE" method applied to the benchmark datasets Fisher's Irises, MNIST and FashionMNIST:
- Given the similarity matrix
 of data points (xi, xj) in the original space, "TSNE" attempts to find the lower-dimensional embeddings
of data points (xi, xj) in the original space, "TSNE" attempts to find the lower-dimensional embeddings  , such that similarities
, such that similarities  in the lower-dimensional space match
in the lower-dimensional space match 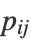 .
. - Similarities in the original space are given by
 , where
, where  corresponds to a neighborhood radius. Similarities in the lower-dimensional space are given by
corresponds to a neighborhood radius. Similarities in the lower-dimensional space are given by  .
. - The lower-dimensional embeddings
 are computed by minimizing the embedding cost
are computed by minimizing the embedding cost  .
. - The parameter
 is indirectly controlled by a perplexity parameter. A large perplexity results in a small amount of clusters while small perplexity leads to many clusters.
is indirectly controlled by a perplexity parameter. A large perplexity results in a small amount of clusters while small perplexity leads to many clusters. - The following suboptions can be given:
-
"Perplexity" Automatic radius ϵ "LinearPrereduction" False whether to perform a linear reduction before running the t-SNE method

Examples
open allclose allBasic Examples (1)
Options (2)
"Perplexity" (1)
Load the Fisher Iris dataset from ExampleData:
Generate a reducer function using the "TSNE" method:
Group the examples by their species:
Reduce the dimension of the features:
Visualize the reduced dataset:
Perform the same operation using a different perplexity value: