"TSNE" （机器学习方法）

详细信息和子选项

  • "TSNE" 代表 t 分布随机邻域嵌入，是一种非线性非参数降维方法. 该方法尝试学习数据的低维表示，以保留数据的局部结构.
  • "TSNE" 适用于具有非线性流形的数据集，特别适用于高维数据集的可视化； 但是，对于具有大量特征和大量示例的数据集进行训练则很慢.
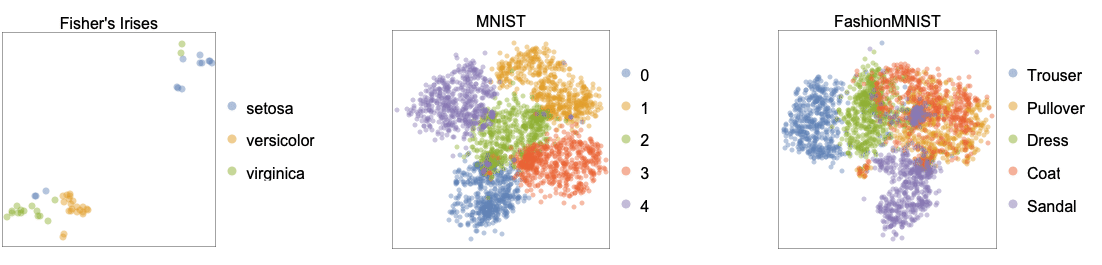
  • 下面显示了 "TSNE" 方法应用于基准数据集 Fisher's Irises、MNIST 和 FashionMNIST 的学习的二维嵌入：
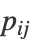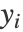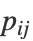  • 给定原始空间中数据点 (xi, xj) 的相似矩阵 p_(ij)，"TSNE" 尝试找到低维嵌入 ，使得低维空间中的 q_(ij) 与 p_(ij) 相匹配.
  • 原始空间中的相似性由 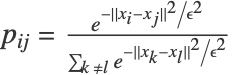给出，其中 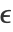对应于邻域半径. 低维空间中的相似性由 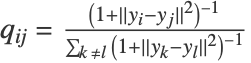给出.
  • 低维嵌入 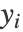通过最小化嵌入成本 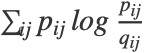计算.
  • 参数 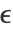由一个困惑度参数间接控制. 困惑度越大，聚类越少，反之亦然.
  • 可以给出以下子选项：
  • "Perplexity" Automatic半径 ϵ
    "LinearPrereduction" False在运行 t-SNE 方法之前是否执行线性缩减

范例

打开所有单元关闭所有单元

基本范例  (1)

使用 "TSNE" 方法降低一些图像的维度：

可视化图像的二维表示：

选项  (2)

"Perplexity"  (1)

从 ExampleData 加载 Fisher Iris 数据集：

使用 "TSNE" 方法生成降维函数：

按物种对示例进行分组：

降低特征的维度：

可视化降维后的数据集：

使用不同的困惑值执行相同的操作：

"LinearPrereduction"  (1)

从 "MNIST" 数据集中加载样本：

使用 "TSNE" 降低图像的维度：

在使用 "LinearPrereduction" 子选项运行 t-SNE 方法之前，通过执行线性缩减来查找特征：

可视化得到的特征并比较结果：

应用  (1)

数据可视化  (1)

使用 "TSNE" 方法降低一些图像的维度：

可视化图像的二维表示：