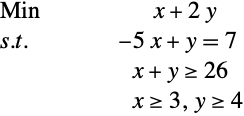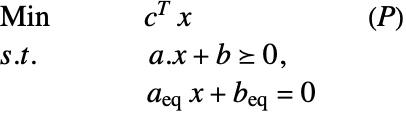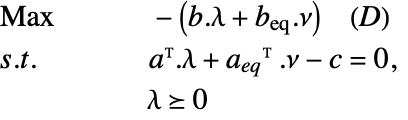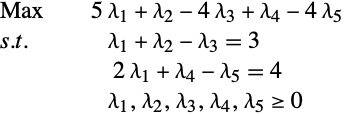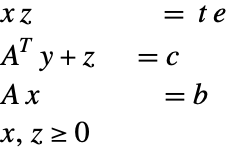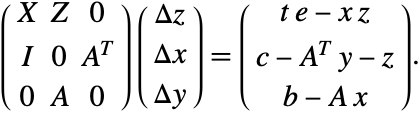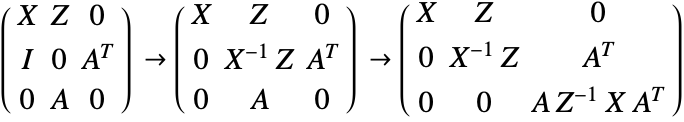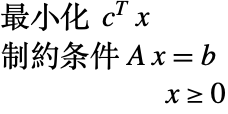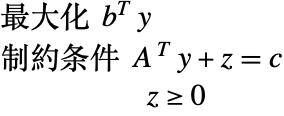線形最適化

はじめに線形最適化の応用例題
LinearOptimization関数線形最適化のアルゴリズム
例題参考文献
大きいデータをインポートし，大規模問題を解く

はじめに

線形最適化問題とは，目的関数と制約条件がすべて線形である問題を言う．

Wolfram言語には実数変数を持つ線形最適化問題を解くためのアルゴリズム群があり，LinearOptimization，FindMinimum，FindMaximum，NMinimize，NMaximize，Minimize，Maximizeでアクセスできる．LinearOptimizationを使うと，線形最適化アルゴリズムに直接アクセスできる．これは使用するメソッドを最も柔軟に指定することができ，大規模な問題に最も効率的である．FindMinimum，FindMaximum，NMinimize，NMaximize，Minimize，Maximizeは方程式および不等式の形式での線形最適化問題を解くのに便利である．

下の線形最適化問題 をMinimizeで解いてみる：
次に，同じ問題をNMinimizeで解いてみる．NMinimizeは機械数の解を返す：
さらに同じ問題をLinearOptimizationで解く：

LinearOptimization関数

LinearOptimization は線形最適化の主要関数であり，使用するメソッドの指定が最も柔軟にでき，大規模な問題に最も効率的である．

線形最適化は，以下の主問題を解く を求める：

最小化する
次の制約条件に従う
ここで

線形最適化のラグランジュ双対問題は以下で与えられる：

最大化する
次の制約条件に従う
ここで

以下のオプションを取ることができる．

オプション名
デフォルト値
MethodAutomatic線形最適化問題を解くのに使用するメソッド
ToleranceAutomatic収束の許容誤差
MaxIterationsAutomatic使用する反復の最大回数
PerformanceGoal$PerformanceGoal最適化を試みる精度
WorkingPrecisionAutomatic内部計算で使用する精度

LinearOptimizationのオプション

Methodオプションは，線形最適化問題を解くアルゴリズムを指定する．これで使用できる値はAutomatic，"Simplex"，"RevisedSimplex"，"InteriorPoint"， "CLP"，"MOSEK"，"Gurobi"である．デフォルトはAutomaticであり，問題の大きさと精度に基づいて，他のメソッドの中から自動的に選ばれる．

Toleranceオプションは，収束の許容誤差を指定する．

WorkingPrecision->Automaticにすると，機械精度でしか動作しないメソッドが指定されていない限り，精度は入力引数の精度から自動的に取られる．そのメソッドが指定されている場合は機械精度が使われる．

LinearOptimizationからアクセスできる解の特性は多数ある：

"PrimalMinimizer"{,…}目的関数を最小化する変数値のリスト
"PrimalMinimizerRules"{v1,…} を最小化する変数 vars={v1,…}の値
"PrimalMinimizerVector"x* を最小化するベクトル
"PrimalMinimumValue" の最小値
"DualMaximizer"
を最大化するベクトル
"DualMaximumValue"双対最大値
"DualityGap"双対問題の最適値と主問題の最適値の差分（強双対性のため0）
"Slack"
制約条件緩和ベクトル
"ConstraintSensitivity"
制約条件摂動への の敏感性
"ObjectiveVector"
線形目的ベクトル
"LinearInequalityConstraints"線形不等式制約条件行列およびベクトル
"LinearEqualityConstraints"線形等式制約条件行列およびベクトル
{"prop1","prop2",...}いくつかの解の特性

LinearOptimizationの解の特性

例題

内点法とシンプレックス法および／または改訂シンプレックス法との違い

シンプレックス法および改定シンプレックス法は，極小値に達するまで目的関数の継続的に小さい方の値で頂点から頂点へと，制約条件により定義されたポリトープの辺に沿って移動することにより線形最適化問題を解く．これらの関数のWolfram言語の実装では，密な線形代数が使われる．この実装のユニークな点は，厳密・拡張精度問題が解けるという点である．したがって，これらの方法は，非機械数の結果が必要ない，または頂点の解が望まれるような小さいサイズの問題に適している．

線形最適化の内点法は，大まかに言うと，制約条件により定義されたポリトープの内部から反復する．これは非常に速く解に近付くが，シンプレックス・改訂シンプレックス法とは異なり，厳密な解は見付けない．Wolfram言語における内点法の実装では，機械精度の疎な線形代数を使う．よって，大規模の機械精度線形最適化問題では，内点法の方が効率がよいのでこれを使うべきである．

以下では，重解（{0,1}と{1,0}の間の線分上にある任意の点が解となる）を持つ線形最適化問題を解く．内点法では，解集合の中央にある解が返される：
SimplexまたはRevisedSimplexを使うと，解集合の境界の解が返される：
以下は，200個の変数のランダムで疎な線形最適化問題では，内点法の方がずっと速く，同様な最適値を与えることを示している：

二重変数の探索

一般的な線形計最適化問題

がある場合，その双対問題は次の通りである．

両方の解が分かっていると便利な場合がある．

主問題と双対問題の解の関係は次の表の通りである．

主問題が…ならば
双対問題は…である
実行可能実行可能
非有界実行不可能または非有界
実行不可能非有界または実行不可能

両方の問題が実行可能である場合，(P)と(D)の最適値は同じであり，主問題の解 および双対問題の解に対して次の相補条件が成り立つ．

双対の最大化はLinearOptimizationで"DualMaximizer"特性を使うことで得ることができる．

次で主問題 の他に，下の双対問題も解く．
双対問題を解いて，結果を確かめる：
以下で主問題と双対が同じ目的値を与えることが確認できる：
主問題と双対問題の目的値を，解の特性を使って直接確認する：
この制約条件 の双対は である．これは，制約条件の右辺が1単位増加すると，最適値は2単位増加することを意味している．このことは，制約条件の右辺を0.001で摂動させることで確認できる：
以下の通り，目的値はその倍増加している：
"ConstraintSensitivity"特性を使って，制約条件 に対する摂動 の影響を見る：

内点法における実行不可能性と非有界性の扱い

主双対内点法は実行可能な問題に対して設計されており，実行不可能／非有界の問題では発散してしまう． その上，現在の実装では発散が実行不可能性によるものか非有界性によるものかを見分けるのは難しい．

ヒューリスティックが実行不可能／非有界の問題を見付け，適切なメッセージを出力する：
ヒューリスティックを使っても，問題が実行不可能／非有界のどちらであるかを確実に見分けることができない場合がある：
Simplexを使うと問題が非有界であることが分かる：

"InteriorPoint"のメソッドオプション

"TreatDenseColumn"は"InteriorPoint"のメソッドオプションであり， 密な列を別々に扱うかどうかを決定する．密な列とは，多くの非零要素を含む制約行列の列のことである．このメソッドのデフォルト値はAutomaticであり，密な列は別々に扱われる．

密な行列を含む大きな問題では特にこのメソッドが便利である：

大きいデータをインポートし，大規模問題を解く

線形最適化問題を記述するのによく使われる形式はMPS（数理計画問題）形式である．これは多数のセクションで構成されるテキスト形式である．

方程式のMPSファイルをインポートする

Wolfram言語はMPS形式のファイルをインポートすることができる．MPSデータのImportにより，線形最適化問題はデフォルトで方程式形式で返される．この形式はLinearOptimization，Minimize，NMinimizeを使って解くことができる．

次でMPSファイル"afiro.mps"で指定された線形最適化問題を解く：

大規模な問題：行列形式およびベクトル形式でのインポート

大規模な問題の場合，MPSデータファイルをインポートし，行列かベクトルで行列問題を表してからLinearOptimizationを使って解いた方が効率的である．

次で，MPS形式のデータで3つの要素がインポートできることを示す：
以下で，1309の制約条件と1681の変数を持つ問題"ganges"をインポートする：
問題を解き，最適値を見付ける：
疎な制約行列だけを求めるときは"ConstraintMatrix"指定を使うことができる：

自由書式のMPSファイル

標準的なMPS形式のファイルでは固定書式が使われており，各欄の文字の位置が厳密に決まっている．しかし，モデリングシステムの中には自由書式のMPSファイルを出力するものもあり，欄の位置が自由である．後者のファイルでは，Importでオプション"FreeFormat"->Trueを指定することができる．

次の文字列は，MPSファイルを自由形式で記述している：
一時的ファイル名を割り当て，それに文字列をエキスポートする：
オプション"FreeFormat"->Trueを使ってファイルをインポートする：

線形最適化テスト問題

NetLib線形最適化テスト問題はすべてExampleData関数からアクセスすることができる．

Netlib集合のすべての問題を見付ける：
問題"afiro"をインポートし，それを解く：
"afiro"問題に対してインポートすることのできる他の特性を表示する：
"afiro"を方程式形式でインポートする：

線形最適化の応用例題

L1ノルム最小化

最小化問題

を，線形最適化問題に変換して解くことができる．

入力と出力の点を定義する：
以下がデータにフィットする：
以下で直線をプロットし，外れ値についてロバストであることを示す：
LeastSquaresを使って得られたフィットと比較する：

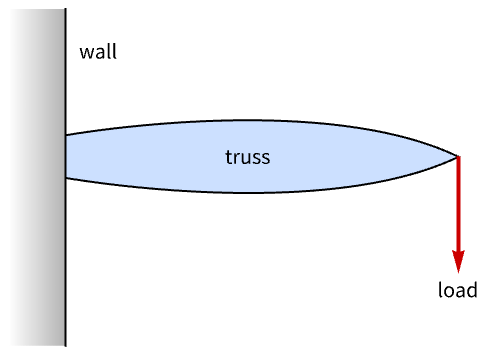
最適なトラスの設計

この例題は[2]から採用したものである．この問題の目的は，負荷をサポートするのにできるだけ少ない材料を使ってアンカーを設計するというものである．

42.gif

この問題は，まずノードとリンクを使って離散化し，シミュレーションを行うことによりモデル化することができる．モデル化の過程は以下の図で示す．ここで7×10のノードを持つ格子が生成される．それぞれのノードはマンハッタン距離が3以下である他のすべてのノードへのリンクにより接続される．赤い3つのノードは壁に固定されるもので，他のノードはすべて圧縮力および張力のバランスが取れていなければならない．

43.gif

各リンクは厚みのある硬い棒を表しており，重さはそれにかかる力と長さに比例している．目標は，使用される材料を最小化することである．

したがって，これは数学的に線形の制約付き最小化問題であり，目的関数が線形関数の絶対値の和である．

目的関数の絶対値は，を圧縮力と張力（ともに非負）に分けて置き換えることができる．ここで をリンクの集合， をノードの集合， をノード と の間のリンクの長さ， と をそれぞれリンク上の圧縮力と張力とすると，上記のモデルは下の線形最適化問題に変換することができる．

トラスが壁に固定されているいくつかの位置を選ぶ．
負荷がかかる位置はトラスの端である．
トラスはリンクとノードを使ってモデル化することができる．各ノードはリンクによって近隣のノードに接続される．接続パターンは以下で与えられる．
候補のノードは矩形格子に置かれる．
ノードの位置，アンカーの位置，力が加わる位置，トラスの中央の単独のノードの接続性を可視化する．
各ノードは一意の指標に関連付けられている．Associationを使うことで迅速にルックアップテーブルが提供される．
アンカーおよび力が加わる点に関連付けられた指標を求める：
指定された接続パターンに対する格子点の接続性を求める関数を構築する．
リンクの集合を で記述する．リンクが ならば でそれ以外は であるという，先ほど定義されたパターンを使って，ノードに対する疎な接続行列 を定義する．
のリンクを記述するには，リンクの指標を使うと便利である．
目的は，を最小化することである．ここで はノード と の間の長さ， は最終の接続点でによって形成されるリンクから働く力である．
関数は非線形であるが，およびとなるようなを導入することによって線形関数として表すことができる．目的は以下になる：
力を受ける点以外の各ノードでは，外部の力は受けない．
力を受ける点では，垂直の下向きの単位力が適用される．
固定されていないそれぞれのノードでは，力の均衡 がある．ここで はノード の位置である．
最終的な制約条件は以下になる．
結果の系を解く．
青がリンクの圧縮を示し，赤がリンクの拡張を示す最適トラスを可視化する．

線形最適化のアルゴリズム

シンプレックス法と改訂シンプレックス法

シンプレックス法と改訂シンプレックス法は，制約条件により定義された多面体の頂点で実行可能解を構築し，その後目的関数のより小さな値を連続的に使い，最小値に達するまでその多面体の辺を頂点に向かって移動させていくことにより最適化問題を解く．

シンプレックス法と改訂シンプレックス法の実装が少ないと実際に非常に効率的であり，大域的最適値が見付かることが保障されているが，最悪の場合には動作に問題が生じる場合もある．構築された線形最適化問題に対して，シンプレックス法と改訂シンプレックス法がその問題の大きさに指数関数的な数のステップを取らなければならなくなる可能性があるのである．

Wolfram言語は密な線形代数を使ってシンプレックス法と改訂シンプレックス法を実装する．この実装のユニークな点は，厳密・拡張精度問題が解けるという点である．従って，これらのメソッドは機械数でない結果が必要とされる小さい問題により適している．

以下で20の制約条件と200個の変数を持つランダムな線形最適化問題を設定する：
この問題を解く．制約条件の数よりも変数の数の方がかなり多い線形最適化問題では，通常改訂シンプレックス法の方が早い．これに反して，変数よりも制約条件の数のほうが多い場合は，シンプレックス法の方が速い：
機械数の結果だけが必要な場合は，問題を機械数の問題に変換し，内点法を使わなければならない：

内点法

シンプレックス法と改訂シンプレックス法は通常非常に効率的であるが，最悪の動作をする場合もある．シンプレックス法と改訂シンプレックス法が問題の大きさに指数関数的な数のステップを取らなければならないような線形最適化問題を構築する可能性があるのである．

さらにWolfram言語ではシンプレックス法と改訂シンプレックス法の実装には密な線形代数が使われるが，内点法の実装には機械数の疎な線形代数が使われる．従って，機械数の大規模な線形最適化問題には，内点法の方が効率的なのでこれを使うべきである．

内点法の公式

標準化された次の線形最適化問題を考えてみる．

ここで ，， である．この問題は，正の制約条件を扱う障壁関数式を使って解くことができる．

上の問題の一階必要条件により，以下が与えられる．

がベクトル からなる対角行列を表し， であるとすると，

が成り立つ．これは制約条件を持つ の線形／非線形方程式の集合である．これはニュートン法

であり

で解くことができる．この線形系を解く方法のひとつに，ガウス消去法を使い行列をブロック三角行列形式に簡約するというものがある．

このブロック三角行列を解くためには，この行列が通常の系に含まれる，いわゆる通常の系を解く．

この行列は正定値行列になるが，解に近付くにつれ非常に悪条件になる．よって解法を安定させるために数値的手法が使われる．通常内点法は，「収束の許容誤差」で説明する許容範囲では，ほぼ付近までの問題を解くよう想定されている．Wolfram言語ではMehrotraの予測子・修正子法[1]が使われている．

収束の許容誤差

一般の線形最適化問題はまず，標準形の

に変換される．ここで対応する双対問題は次の通りである．

内点法の収束条件は

であり，許容範囲はデフォルトでに設定されている．

参考文献

[1] Vanderbei, R. Linear Programming: Foundations and Extensions. Springer-Verlag, 2001.
[2] Mehrotra, S. "On the Implementation of a Primal-Dual Interior Point Method." SIAM Journal on Optimization 2 (1992): 575–601.