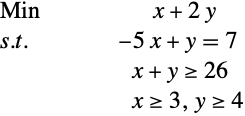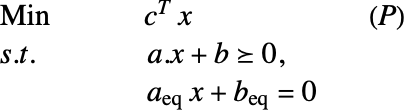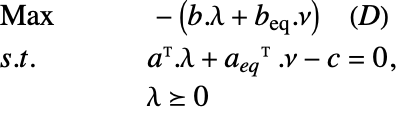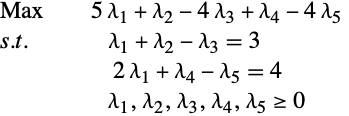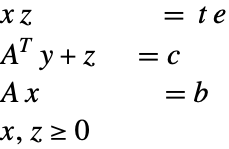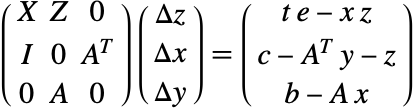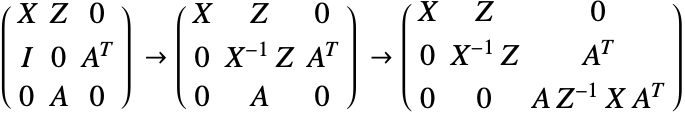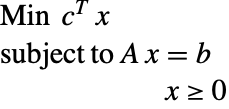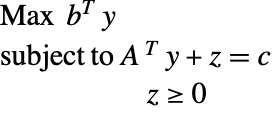线性优化
引言
Wolfram 语言收集了大量的算法来解决实变量的线性优化问题，这些算法都可通过 LinearOptimization、FindMinimum、FindMaximum、NMinimize、NMaximize、Minimize 和 Maximize 调用执行. LinearOptimization 对各种线性优化算法提供直接的支持，并提供了最灵活的方式来指定使用哪个算法，而且能够最有效地解决大规模问题. FindMinimum、FindMaximum、NMinimize、NMaximize、Minimize 和 Maximize 对求解等式和不等式形式的线性优化问题更为方便.
LinearOptimization 函数
LinearOptimization 是线性优化问题的主要函数，它能够最灵活地指定应该使用哪一个函数，并且对于解决大规模问题是最有效的.
选项名
|
默认值
| |
| Method | Automatic | 解决线性优化问题采用的方法 |
| Tolerance | Automatic | 收敛容差 |
| MaxIterations | Automatic | 使用的最大迭代次数 |
| PerformanceGoal | $PerformanceGoal | 优化的目标 |
| WorkingPrecision | Automatic | 内部计算使用的精度 |
Method 选项用来指定求解线性优化问题所使用的算法. 可能的值包括 Automatic、"Simplex"、"RevisedSimplex" 、"InteriorPoint"、 "CLP"、"MOSEK" 和 "Gurobi". 默认值是 Automatic，可以根据问题的大小和精度需要从其他方法中自动选择合适的算法.
Tolerance 选项可以用来指定收敛容差的大小.
当设置为 WorkingPrecision->Automatic 时，精度是从输入参数的精度自动获取的，除非指定的方法仅适用于机器精度，在这种情况下使用机器精度.
可通过 LinearOptimization 函数获取许多解的属性：
| "PrimalMinimizer" | { ,…} | 一个最小化目标函数的变量值列表 |
| "PrimalMinimizerRules" | {v1 ,…} | 最小化  的变量值 vars={v1,…} |
| "PrimalMinimizerVector" | x* | 最小化  的向量 |
| "PrimalMinimumValue" |  | 最小值  |
| "DualMaximizer" |  | 最大化 
|
| "DualMaximumValue" |  | 对偶最大值 |
| "DualityGap" |  | 对偶值和原始最优值之间的差（由于强对偶性，差应为 0） |
| "Slack" | 
| 约束松弛向量 |
| "ConstraintSensitivity" | 
|  对约束条件扰动的敏感性 |
| "ObjectiveVector" | 
| 线性目标向量 |
| "LinearInequalityConstraints" |  | 线性不等式约束矩阵和向量 |
| "LinearEqualityConstraints" |  | 线性等式约束矩阵和向量 |
| {"prop1","prop2",...} | | 解的几个属性 |
LinearOptimization 的解的属性.
例子
内点法和单纯形法和/或修正单纯形法的区别
单纯形法和修正单纯形法通过以下方法解决线性优化问题: 沿着约束条件所定义的多面体边缘移动，从一个顶点到达另一个顶点，以使得目标函数值逐渐减小，直至达到最小值. Wolfram 语言通过稠密线性代数实现单纯形法和修正单纯形法. 这种实现方法的独特之处在于它有可能解决精确/扩展精度问题. 因此，这些方法对于需要非机器精度结果的小规模问题或者当我们期待得到一个在顶点上的解时更为适用.
笼统地说，线性优化的内点算法是从约束条件定义的多面体的内部依次迭代的. 它们可以非常快地接近问题的解，但是与单纯形法/修正单纯形法不同的是，他们不能精确地找到解. Wolfram 语言利用机器精度稀疏线性代数执行内点法. 因此，对于大规模机器精度线性优化问题，内点法更为有效，更为适用.
寻找对偶变量
如果原始问题是
|
那么对偶问题是
|
| 可行 | 可行 |
| 无界 | 不可行或者无界 |
| 不可行 | 无界或者不可行 |
当这两个问题都是可行的时候，(P) 和 (D) 的最优值是相同的，并且下面的补充条件对于原始问题的解 
和对偶问题的解 
是成立的.
可通过解的 "DualMaximizer" 属性从 LinearOptimization 获取对偶最大值点.
处理内点法中的不可行性和无界性
原始-对偶内点法是为可行问题而设计的；对于不可行/无界问题，它是发散的，而在目前的执行过程中，我们很难查明发散是由于不可行性，还是由于无界性.
"InteriorPoint" 的方法选项
"TreatDenseColumn" 是 "InteriorPoint" 的一个方法选项，它决定对稠密列是否要分别处理. 稠密列指的是具有许多非零元素的约束矩阵的列. 在默认情况下，该方法选项的值为 Automatic，此时分别处理稠密列是分别处理的.
导入大型数据集和求解大规模问题
一个用于记录线性优化问题的常用格式是数学规划系统 (MPS) 格式. 这是一个包含若干章节的文本格式.
以方程形式导入 MPS 格式文件
Wolfram 语言可以导入 MPS 格式的文件. 默认情况下，MPS 数据的 Import 返回一个方程形式的线性优化问题，这样就可以通过使用 LinearOptimization、Minimize 或者 NMinimize 求解.
大规模问题：以矩阵和向量形式导入
对于大规模问题，导入 MPS 数据文件并用矩阵和向量表示线性优化问题，然后用 LinearOptimization 求解更有效.
自由格式的 MPS 文件
标准格式的 MPS 文件采用一个固定的格式，其中每个域占有一个严格固定的字符位置. 然而，一些建模系统以自由格式输出 MPS 文件，其中每个域自由地放置. 对于这种文件，对 Import 可以选用选项"FreeFormat"->True.
线性优化测试问题
通过 ExampleData 函数，所有 NetLib 线性优化测试问题都可以被访问.
线性优化问题的应用实例
L1-范数最小化
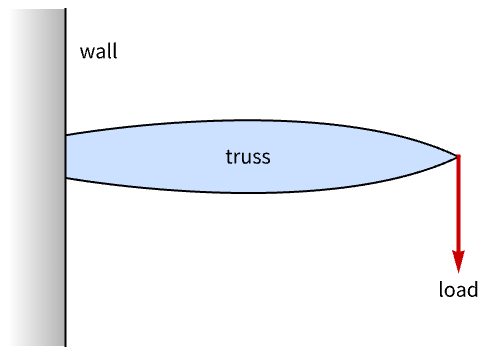
一个最优桁架的设计
这个例子是从 [2] 中引入的. 目的是要设计一个锚，使用尽可能少的材料来支撑负载.
这个问题可以通过离散化并用节点和链路对其进行模拟来建模. 建模过程通过下面的图标显示. 在此一个具有7×10个节点的网格被产生. 每个节点通过链路与所有其他曼哈顿距离小于或等于三的节点链接. 三个红色节点假设固定在墙上，而在所有其他节点上，压力和张力必须平衡.
每个链路代表一个具有一定粗细的刚性棒，其重量和它上面的力以及它的长度成正比. 我们的目的是最小化使用的材料总量，即:
因此从数学理论上看，这是一个线性约束极小化问题，其目标函数是线性函数绝对值的和.
目标函数中绝对值 
可以通过把 
分成压力和张力的组合来代替，其中每个项都是非负的. 因此假设 
是链路的集合，
是节点的集合，
是节点 
和 
之间的链路长度，而 
和 
是链路上的压力和张力；那么上述模型可以被转化为一个线性优化问题.
线性优化的算法
单纯形法和修正单纯形法
单纯形法和修正单纯形法通过以下方法求解线性优化问题：先在约束条件所定义的多面体的一个顶点构造一个可行解，然后沿着该多面体边，从一个顶点移动到另一个顶点，以使得我们的目标函数值逐渐减小，直至达到最小值.
虽然单纯形法和修正单纯形法的稀疏实现方法在实践上很有效，并且能够保证找到全局最优解，该算法有一个很差的最坏情况下的行为表现：即有可能会建立这样一个线性优化模型，使得单纯形法和修正单纯形法的步骤数目与问题大小呈指数关系.
Wolfram 语言通过稠密线性代数实现单纯形法和修正单纯形法. 这种实现方法的独特之处在于它有可能可以解决精确/扩展精度问题. 因此，这些方法对于需要非机器精度结果的小规模问题更为适用.
内点算法
虽然单纯形法和修正单纯形法平均上看可以非常有效，可是它们最差情况下的行为却很糟糕. 我们有可能会建立一个线性优化模型，其中单纯形法和修正单纯形法的步骤数目随问题大小呈指数增长. 而内点算法收敛所需的步骤数目已经被证明随问题大小呈多项式变化.
此外，Wolfram 语言的单纯形法和修正单纯形法的实现利用稠密线性代数，而它的内点法的实现利用机器精度的稀疏线性代数. 因此对于大规模，机器精度线性优化问题，其内点法更为有效并且更应该使用.
内点法表述
其中 
、
、
. 这个问题可以通过使用障碍函数方法来处理正值约束来求解.
这是一个由 
个有约束条件的线性/非线性方程组成的集合. 它可以使用牛顿法
求解这个线性系统的一个方法是使用高斯消去法把矩阵简化成块三角矩阵的形式.
为了求解这个块三角矩阵，我们可以求解所谓的正规系统，该正规系统中的矩阵：
这个矩阵是正定的，但是当接近我们要求的解时就变得非常病态了. 因此我们使用数值技术来稳定求解的过程，并且通常情况下我们只能期待内点法求解该问题到一个大约为 
的容差，容差的概念在 "收敛容差" 中有解释. Wolfram 语言使用 Mehrotra 的预估校正方案 [1].
