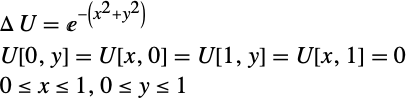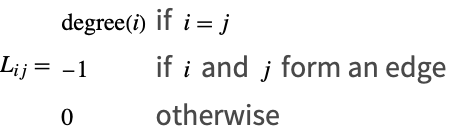最新のWolfram言語には，このチュートリアルに関連する新機能が追加されている．最新情報は行列と線形代数を参照のこと．

線形代数の例題

行列の並べ替え有限差分解法
最大階数最小二乗解メッシュ区分
1-ノルムと無限ノルムの最小化NDSolveを使った行列関数

このチュートリアルでは，線形代数を含むWolfram言語による計算の例を多数紹介する．

行列の並べ替え

疎行列技術によっては行列を並べ替え，要素をブロックにグループ化されるように試みる．その後各ブロックごとに密行列技術を使って計算が行われる．行列をブロックに並べ替える簡単な方法のひとつに，各行の要素の総和によってソートするというものがある．これを以下に示す．

まず，対称な乱数疎行列を作成する：
行列をプロットする：
行列の置換を計算し，それを行列に適用する．これについては「行列の置換」で述べた：
並べ替えられた行列は以下のようになる．図から並べ替えの効果が分かる：
構造がなく，乱数の要素がたくさんある，はるかに大きい行列を考える：
もとの行列をプロットする：
並べ替えられた行列のプロットから，要素がない行・列がたくさんあることが分かる：

最大階数最小二乗解

行列方程式 を解くことは，行列計算の需要な問題のひとつである．その解法については「線形系の解法」で述べた． が× の行列なら， 個の未知数を持つ 個の線型方程式一式である． の場合は，方程式の数が未知数の数より多い過剰決定系である．最小二乗解を求める一般的な方法は「最小二乗法」で述べた．以下の例では，最大階数行列の過剰決定系の適切な解の別の求め方をいくつか紹介する．

このセクションの例題の解法は，入力として疎行列を与えたときにのみ正しく動作することに注意されたい．

最小二乗コレスキー

この方法は最小二乗解を求めるのに「コレスキー分解」を使う．行列 が最大階数を持つなら，解は以下のようにして求められる．

これらのステップは以下のようにしてWolfram言語関数に埋め込む：
この関数は次のようにして使用する：
求められた解は近く，方程式を満足する：
PseudoInverseで求められる解と比較する：

この方法は早いが， を計算するため正確ではない．

求められた解の1-，2-，ノルムを計算する：

最小二乗QR

が最大階数の場合，問題をより正確に解くにはQR分解を使う．これを以下に示す．

解を求めるWolfram言語プログラムは以下のようになる：
この問題の解はコレスキー解とよく似ている：
QR分解の解はコレスキー法よりコストが高くなるが，より正確である．その差を以下に示す：
2-ノルムを使うとコレスキー解がどのくらい近くなるかを調べる：
2-ノルムを使うとQR解がどのくらい近くなるかを調べる．QR分解の方がよりよい近似であることが分かる：

1-ノルムと無限ノルムの最小化

行列方程式 が過剰決定形()の場合に，近似解を求める方法の多くでは，2-ノルムの最小化を行う．これは計算的に扱いやすくなる利点があるからである．ひとつの理由は，関数

が微分可能で，微分が線形操作であるということである．そのため，最小の解を求める線形系が形成できる．もうひとつの理由は，直交変換において2-ノルムが維持されるということである．これは，解くのがより簡単である可能性がある同様の問題が幅広く形成できるということを意味している．

しかし，1-ノルムや-ノルム等，他のノルムを最小化することで見つかる他の解も存在する．これらは，解が個々の問題に関する重要な性質を維持する可能性があるので，特定の状況において，より望ましいことがある．次の例では，これらのノルムを最小化する近似解を求める方法を示す．両方とも制約付き線形問題の最小値を求める方法を使う．これは特に線形計画法として知られる．

Wolfram言語では，線形計画法の解法には関数LinearProgrammingが使える．これを使うと，整数，有理数，機械精度の近時実数，任意精度の近似実数等，Wolfram言語がサポートしている種々の型の数の線形計画問題が解ける．さらに，内点法を使って，特に大規模な系を最小化するのに適した方法も利用できる．

このセクションで与えられている解法は，入力が密行列の場合に適している．これを疎行列用に変更するのは簡単である．これは内点線形計画法を十分に利用するために必要である．

このセクションで述べる方法は，解の他の制約を加えて拡張することもできる．

1-ノルム最小化

1-を最小化する際は，次の式を最小化する の値を求める．

これは新しい変数 を形成し，最小値を求めることで行える．

以下はこれを実装するプログラムである：
解を求める：
求められた解の1-，2-，ノルムを計算する：

無限ノルムの最小化

-ノルムの最小化は1-ノルムの最小化と似ている．以下を最小化する の値を求める．

これは新しい変数 を形成し，最小値を求めることで行える．

以下はこれを実装するプログラムである：
解を求める：
求められた解の1-，2-，-ノルムを計算する：

有限差分解法

偏微分方程式を解くひとつの方法に，特別な離散化を行い，有限差分で解くというものがある．次の例で，単位正方形における基本的なポアソン(Poisson)方程式の差分解法を考える．

である80×80のグリッドの問題を設定する．変数行列が簡約された形で表示される：
差分演算子の有限差分方程式である：
ここで，変数行列の有限差分方程式の用途を作る．境界条件は境界付近のゼロ係数を持つ変数のひとつのオーバーハングを受け入れることで統合される：
グリッド上の解の方程式を形成する：
ポアソン方程式の近似解は，これらの方程式を解くと求められる．方程式を解くひとつの方法は，Solveを使うことである．Solveは方程式を線形かつ疎なものであると認識し，疎行列ソルバを使用する．別のポアソン問題が解ける可能性のあるもうひとつの方法は，方程式から行列を作ることである．グリッドがベクトルに平坦化されると，行列は線形演算子を表す：
LinearSolveを使うと，解が素早く求められる：
もとの構造を維持するために，解を再区分する：
解の等高線プロットを作成する：
同じ形状寸法で，右辺の関数は異なる場合に複数のポアソン方程式を解くには，行列の分解を計算し，それを繰返し使用する．Wolfram言語で行列の分解を繰返し行う方法は「行列の分解の保存」で述べた：
グリッド上で関数Cos[6x2+3y2]を表すベクトルを与える：
ベクトルを分解し，解が得られる：
この解は領域内の離散点においてのみ得られる．境界や領域内の他の点の値は含まれない．解が他の計算で使われるなら，制約が生じることがある．PadLeftとPadRightを使うと境界地を加えることができ，Interpolationを使うと領域の補間関数を生成することができる：
Plot3Dを使って解をプロットする：
領域内のどの点でも解が計算できるようになった：

メッシュ区分

ここでは，固有値の実践的な使用方法を例示する．目的はメッシュ／グラフの頂点を2つのサブ領域に分割し，各部分の頂点の数をおおよそ同じにし，その境界が辺を切断するのをなるべく少なくするというものである（2つの頂点が別々のサブ領域にあると，辺は切断される）．ラプラシアン(Laplacian)を作成し，そのフィードラー(Fiedler)ベクトル（2つ目に小さい固有値に相当する固有ベクトル）を使って頂点を並べるというものがある．これらはグラフ区分において，より効率的な方法であり，固有ベクトルの計算は必要ないが，フィードラーを使う方法は重要である．

データ

頂点座標のデータである：
次はメッシュを形成する三角形のリストである：

メッシュのプロット

メッシュは，各三角形をプロットするとプロットできる：

ラプラシアン

グラフ のラプラシアンは，× の疎行列である． はグラフ中の頂点の数である． の要素のほとんどはゼロであるが，対角要素は正の整数で，これは頂点の次数に対応している．ここで次数とは，ひとつの頂点につながっている他の頂点の数である．また，頂点 ， が辺でつながっている場合，要素 は-1である．

ここでのメッシュでは，非対角要素は疎配列 で与えられる：
行の中の対角要素は非対角要素の和の正負を逆にしたものである．したがって，行列の対角要素は次のようになる：
ラプラシアンは以下のようになる：
行列を可視化する：

フィードラー(Fiedler)ベクトル

各行の要素の総和はゼロであるので，ラプラシアン行列は固有値がゼロの準正定値行列である．2つ目に小さい固有値に対応する固有ベクトルはフィードラーベクトルと呼ばれる．

固有値と固有ベクトルの最小のものから2つを求める：
固有値の1つはゼロである：

ノードの区分

フィードラー固有ベクトルを使ってベクトルの順序を求め，2つの頂点のグループdomain1とdomain2を形成する：
domain1の頂点の色をHue[0.]（赤），domain2の頂点の色をHue[0.75]（青）に設定する：
区分をプロットする．メッシュの特に密度の高い部分を避けるように区分され，各サブ領域はうまくつながっている：
区分により辺が切断される回数は以下のようにして求められる：

NDSolveを使った行列関数

Wolfram言語の数値ソルバの重要な機能のひとつに，入力がベクトルや行列でも使えるということが上げられる．一般にこれは連立方程式の解法に使われるが，行列特有の問題の解法にも使える．ここでは，数値微分方程式ソルバNDSolveを使って行列関数のパラメータかされた解を求める例を示す．

3×3の行列がある：

微分方程式の解は指数関数である．

これは方程式を記号的に解くことで示せる：
行列方程式を形成しNDSolveで解くと，行列の指数Exp[A t]が求められる．ここでの解はのときにだけ有効である：
解は t についての行列関数Exp[A t]を返す関数である．t が0.0なら，単位行列が返される：
Exp[A].Exp[A ]=Exp[2A]であることを示す：
Wolfram言語には関数の指数を計算する関数MatrixExpがある．これは求められた解と比較できる：
Sin関数の微分方程式がある：
行列 A のSinを計算する：
行列のSinは原点では正しい：
行列 A のCosを計算する：
行列のCosは原点では正しい：
において恒等式が成り立つことを示す：