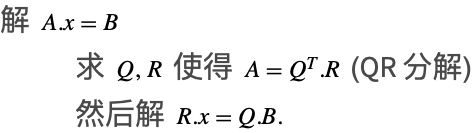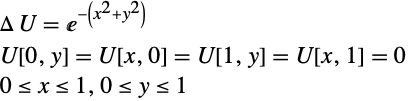在 Wolfram 语言的后续版本中引入了与本教程内容相关的附加功能. 最新信息请见矩阵和线性代数.

线性代数的例子

矩阵排序有限差分解
满秩最小二乘解网格分区
1-范数和无穷-范数的最小化带有 NDSolve 的矩阵函数

本教程展示了一些使用 Wolfram 语言 进行涉及线性代数的计算的例子.

矩阵排序

某些稀疏矩阵技术尝试对矩阵重新排列，使元素组合成块. 然后利用高密度矩阵技术计算每个矩阵块. 一个简单的对矩阵按块排序的方式，涉及到按照每行元素的总和排序. 这将在这个例子中说明.

首先，生成一个对称随机稀疏矩阵：
这是该矩阵的图形：
现在，计算矩阵的排列，然后将其应用到矩阵. 关于这个主题的讨论见"矩阵排列"：
这是重新排序后矩阵的图形，从图中可以看到重新排序的效果：
这里是一个无结构并含有许多随机元素的更大的矩阵：
这是初始矩阵的图形：
重新排序后矩阵的图形表明，矩阵有很多没有元素的行和列：

满秩最小二乘解

求解矩阵方程 是矩阵计算的关键问题之一；关于求解技巧在"求解线性系统"中有讨论. 如果 是一个 × 矩阵，这是由含有 个未知数的. 如果 ，即方程个数大与未知数个数，则方程组是超定系统. 一种用于找到最小二乘解的一般技巧在"最小二乘解集"中给出. 这个例子将展示一些不同的技术来找到满秩矩阵超定系统的近似解.

请注意对于本节所有例子中的解同样适用于在输入中给出稀疏矩阵的情形.

最小二乘 Cholesky

这个技巧采用 Cholesky 分解找到最小二乘解. 如果一个矩阵 有满秩，可以通过以下方式找到解.

这些步骤可以按以下方式放到 Wolfram 语言 函数中：
该函数的应用如下：
解接近于满足方程：
将解与通过 PseudoInverse 得到的解比较：

这个技术速度快，但由于计算 使得它的准确性较低.

这里计算该解1范数，2范数，和 范数：

最小二乘 QR

当 是满秩时，一种更准确的解决该问题的方法是使用如下的 QR 分解.

下面是一个找到该解的 Wolfram 语言 程序：
这个问题的解与 Cholesky 解非常相似：
QR 分解得到解的代价远高于 Cholesky 方法，但准确性更高. 下面的例子显示了这种准确性的差异：
这里说明当使用2范数时 Cholesky 解的接近程度：
这里说明当使用2范数时 QR 解的接近程度. 可以看到 QR 解近似性较好：

1-范数和无穷-范数的最小化

当矩阵方程 超定（即 ）时，找到近似解的许多技术要进行2范数最小化. 这是由于使得它在计算上易于处理的一定的优势. 原因之一是，函数

是可微的，并且微分是一个线性操作. 因此，可以构成一个找到最小解的线性系统. 另一个原因是，在正交变换下2范数可以保存. 这意味着可以构成一系列可能比较易于求解的等价问题.

然而，还可以通过最小化其它的范数，例如1范数或范数，来找到另外的解. 在某些特定情况下，这些方式可能会由于找到的解能够保持一些相对于个别问题的重要性质，从而更可取. 在这个例子中展示了一些技术来找到使范数最小化的适当解； 两者都将使用一个方法来寻找约束线性问题的最小值；这通常被称为线性编程.

在 Wolfram 语言 中，线性编程由函数 LinearProgramming 实现. 它可以解决对 Wolfram 语言 所支持的不同类型的数值的线性编程问题：这些数值类型包括整数、有理数，以及机器精度近似实数和任意精度近似实数. 另外，它还通过内点法来提供适当的技术来使极大型系统最小化.

在本节中给出的解适用于密集矩阵的输入. 将这些解进行修改可直接作为稀疏矩阵输入，这将有必要充分利用内点法线性编程技术.

注意本节中的这些技术可以进行扩展，在解中加上其它约束.

1-范数最小化

最小化1范数需要找到使下式最小化的 的值.

这通过产生新变量 并找到最小值实现.

这通过下述程序执行：
找到了解：
这里计算所找到的解的1范数、2范数和范数：

无穷-范数最小化

范数的最小化与1范数的最小化相似，涉及到找到使下式最小的 的值.

这通过产生新变量 并找到最小值实现.

这通过下述程序执行：
找到了解：
这里计算所找到的解的1范数、2范数和范数：

有限差分解

求解偏微分方程的一种方式是，形成一个空间离散并求其有限差分解. 这个例子考察一个单位正方形上的泊松方程的基本有限差分解.

这里将问题设置到一个 80×80 的网格上，其中 . 变量矩阵的缩略形式被显示出来：
这是微分算子的有限差分公式：
在这一步，将有限差分公式应用于变量矩阵. 通过允许边界附近一个系数为零的变量的过剩，边界条件被纳入：
这里形成了网格上解的方程：
泊松方程的近似解将通过求解这些方程得到. 求解这些方程一种方式是使用 Solve，方程将被识别为线性和稀疏方程，并相应使用一种稀疏矩阵求解程序. 另外一种同样能够求解附加泊松问题的方式是由方程构建一个矩阵. 当网格被拉平至一个向量时，该矩阵将代表线性算子：
现在使用 LinearSolve，解被迅速找到：
这里重新对解进行分区，以恢复原始结构：
这里作出解的等高线图：
如果想要求解几个具有相同几何性质但不同右手函数的泊松方程，您可以计算矩阵的分解，并将其用反复使用. Wolfram 语言 所允许的重复分解方式将在 "因式分解的保存" 中介绍：
现在您只需要给出一个向量来表示网格上的函数 Cos[6x2+3y2]：
这里将该向量传递给因式分解，然后找到解：
应该注意到这个解仅存在于区域内部的离散点上. 这不包括边界上或内部的其它点上的值. 要是这个解用于其它计算目的的话，可能会存在一个限制. PadLeft 和 PadRight 可用于增加边界值，Interpolation 用于生成该区域的一个差值函数：
使用 Plot3D 绘制出解：
现在可以在这个区域的任何位置进行解的计算：

网格分区

这个例子演示了一个极端特征值的实际用途. 其目的是将网格或图形的顶点分割为两个子域，各自含有数量大致相等的顶点，分区贯穿尽可能少的边缘.（边缘在当它的两个顶点分别在每个子域上被削去.）对图形分区的一种方式是形成拉普拉斯并使用其费德勒向量（对应第二最小特征值的特征向量）以对顶点排序. 对图形分区还存在更高效的算法，不需要进行特征向量的计算，但是费德勒方法仍然是重要的一种方法.

数据

这是顶点坐标的数据：
这是形成网格的三角形列表：

绘制网格

绘制网格仅需绘出每一个三角形：

拉普拉斯算符

一幅图形的拉普拉斯算符，，是一个 × 离散矩阵，在图形中有 个顶点. 的输入值大多为零，对角线是与顶点次数对应的正整数，这里次数指的是与该顶点相连的顶点的个数. 另外，如果两个顶点， 和 通过一条边相连，则 为 -1.

对于这里的网格，对角线外的元素通过稀疏矩阵 给出：
一行中的每一个对角线元素是对角线外元素的总和的相反数. 因此，矩阵对角线部分如下：
因此，拉普拉斯算符按下面所示给出：
这里将矩阵可视化：

费德勒向量

每一行之和为零，因此拉普拉斯算符矩阵是具有零特征值的正半定矩阵. 对应于第二最小特征值的特征向量称为费德勒向量.

计算两个最小的特征值和特征向量：
其中一个特征值是零：

节点的分区

现在使用费德勒向量生成顶点的排序并形成两组顶点：domain1 和 domain2：
这里将顶点在 domain1 的颜色设置为 Hue[0.] (红)，在 domain2 的颜色设置为 Hue[0.75] (蓝)：
将分区进行绘制. 可以看出，分区避免了网格的过度密集，并且每个子域被很好地连接：
通过分区所削去的边的个数可以按以下方式进行计算：

带有 NDSolve 的矩阵函数

Wolfram 语言 的诸多数值求解程序的重要特征之一是它们适用于向量和矩阵输入. 通常这用于求解耦合方程组，但也可用于解决矩阵特有的问题. 这里将给出一个使用数值微分方程求解程序 NDSolve 来找到矩阵函数的参数化解的例子.

这是一个 3×3 矩阵：

指数函数是微分方程的解.

这可以通过符号求解方程进行演示：
该矩阵幂 Exp[A t] 可以通过形成一个矩阵方程并使用 NDSolve 求解得到. 这里的解在 时有效：
该解是一个函数，将返回 t 在一定范围内的矩阵函数 Exp[A t]. 如果 t 是 0.0，则返回恒等式矩阵：
这里展示了 Exp[A]：Exp[A ]=Exp[2A]：
Wolfram 语言 已有函数 MatrixExp 用于计算一个函数的指数. 可以与计算得到的解进行比较：
这是 Sin 函数的一个微分方程：
计算矩阵 A 的正弦 Sin ：
矩阵的 Sin 在原点处有正确的行为：
计算矩阵 A 的余弦 Cos：
矩阵的 Cos 在原点处有正确的行为：
这里展示恒等式 , 其中 ：