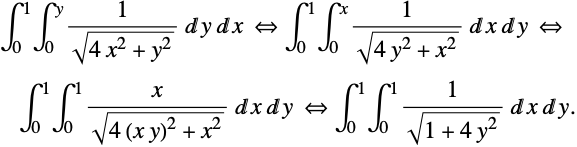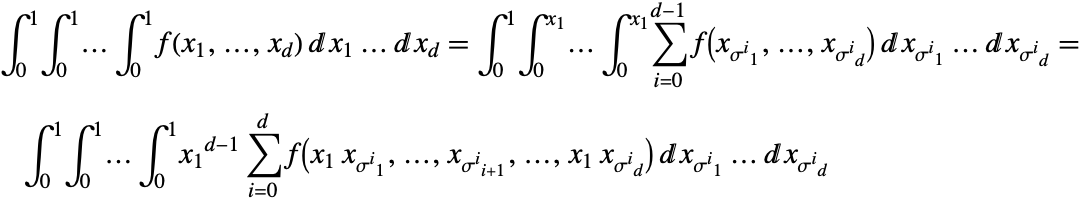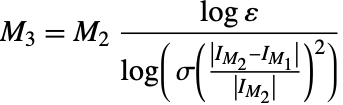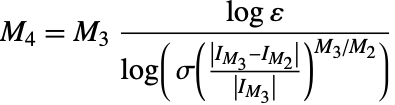NIntegrate積分ストラテジー

はじめに有限領域振動積分
適応型ストラテジー外挿振動ストラテジー
大域的適応型ストラテジー二重指数関数型振動積分
局所的適応型ストラテジー単純モンテカルロストラテジーと準モンテカルロストラテジー
"GlobalAdaptive"と"LocalAdaptive"大域的適応型モンテカルロストラテジーと準モンテカルロストラテジー
特異点の処理"MultiPeriodic"
二重指数関数型ストラテジープリプロセッサ
"Trapezoidal"ストラテジー例題と応用
振動ストラテジー

はじめに

積分ストラテジーとは，ユーザ指定の目標精度あるいは目標確度を満足する積分推定値を計算しようと試みるアルゴリズムである．

積分ストラテジーは，通常初期積分領域の非隣接部分領域集合の新しい要素を生成し管理する方法を指示する．それぞれの部分領域にはそれ自体の被積分関数とそれに関連付けられた積分則がある場合がある．積分推定値はすべての部分領域の積分推定値の総和である．積分ストラテジーは積分則を使い，部分領域の積分推定値を計算する．積分則はサンプル点（または分点）と呼ばれる点の集合における被積分関数をサンプリングする．

積分推定値を向上させるためには，被積分関数をもっと多くの点でサンプリングしなければならない．それには2つの主な方法がある．(i)1つ目は適応型ストラテジーと言い，これは問題のある積分部分を見付け，それに対して計算努力（サンプル点）を集中させる．(ii)2つ目は非適応型ストラテジーで，領域全体のサンプル点の数を多くし，以前の積分推定値の被積分関数の評価を再利用する，高次の積分則推定値を計算するものである．

どちらのアプローチも，より速く収束させるために記号的前処理，変数変換あるいはシーケンス総和加速を使うことができる．

下の積分では，NIntegrateの記号的区分プリプロセッサが，被積分関数を区分関数として認識する．積分は の領域では被積分関数で，の領域では被積分関数で実行される：
以下は積分で使用されたすべてのサンプル点のプロットである．被積分関数は y 座標の順に x 座標でサンプリングされる．サンプル点が特異点付近に集中しているのが分かる．プロット上部のサンプル点で形成されるパターンはプロットの下部のパターンとは異なる．これは特異点ハンドラが適用されるためである：

セクション「適応型ストラテジー」には，適応型ストラテジーの一般的な説明がある．NIntegrateのデフォルト（主）ストラテジーは"GlobalAdaptive"であり，これについては「大域的適応型ストラテジー」で説明している．これと相補的であるのが「局所的適応型ストラテジー」で説明している局所的適応型ストラテジーである．どちらの適応型ストラテジーも「特異点処理」で説明する特異点処理メカニズムを使用する．

モンテカルロストラテジーは，セクション「単純モンテカルロ法と準モンテカルロ法」および「大域的適応型モンテカルロストラテジーと準モンテカルロストラテジー」で説明してある．

"GlobalAdaptive"任意の被積分関数，適応型サンプリング，規則ベース
"LocalAdaptive"任意の被積分関数，適応型サンプリング，規則ベース
"DoubleExponential"任意の被積分関数，一様サンプリング
"Trapezoidal"任意の被積分関数，一様サンプリング
"MultiPeriodic"多次元被積分関数，一様サンプリング
"MonteCarlo"任意の被積分関数，一様ランダムサンプリング
"QuasiMonteCarlo"任意の被積分関数，一様擬似乱数サンプリング
"AdaptiveMonteCarlo"任意の被積分関数，適応型乱数サンプリング
"AdaptiveQuasiMonteCarlo"任意の被積分関数，適応型擬似乱数サンプリング
"DoubleExponentialOscillatory"一次元無限範囲の振動被積分関数
"ExtrapolatingOscillatory"一次元無限範囲の振動被積分関数

NIntegrateの積分ストラテジー

NIntegrateは特殊な型の積分（あるいは被積分関数）に対して，一定のプリプロセッサストラテジーを使う．これについてはそれぞれ「Duffyの座標ストラテジー」，「振動ストラテジー」，「コーシー(Cauchy)の主値積分」で説明する．プリプロセッサストラテジーもまた被積分関数の記号的前処理を扱う．

"SymbolicPreprocessing"全体的なプリプロセッサ制御子
"EvenOddSubdivision"偶関数および奇関数の被積分関数を簡約化する
"InterpolationPointsSubdivision"補間関数を含む被積分関数を部分分割する
"OscillatorySelection"振動する被積分関数を検出し，適応したメソッドを選ぶ
"SymbolicPiecewiseSubdivision"区分関数を含む被積分関数を部分分割する
"UnitCubeRescaling"多次元の被積分関数を単位立方体に再スケールする
"DuffyCoordinates"多次元の特異点除去変換
"PrincipalValue"コーシー主値と等価の数値積分

NIntegrateのプリプロセッサストラテジー

適応型ストラテジー

適応型ストラテジーは，被積分関数が非連続であったり，被積分関数に他の種類の特異性がある部分に計算努力を集中させようとする．適応型ストラテジーは，積分領域を非隣接の部分領域に分割する方法が異なる．各部分領域の積分値は積分値全体に影響を与える．

適応型ストラテジーの基本的な前提は，指定された積分則 と被積分関数 がある場合，積分領域 が2つの非隣接部分領域 と （ここで ，）に分割されるならば，と 上の の積分推定値の総和は実際の積分 により近くなるということである．つまり

であり，(1)は および に対する誤差推定値の総和は の誤差推定値よりも小さいことを意味している．

したがって，適応型ストラテジーには以下のようなコンポーネントがある[MalcSimp75]．

(i) 領域上の積分および誤差推定値を計算するための積分則

(ii) 領域集合のどの要素を分割・部分分割するかを決定するメソッド

(iii) 適応型ストラテジーアルゴリズムをいつ終了するかを決定するための終了基準

大域的適応型ストラテジー

大域的適応型ストラテジーは最大誤差を持つ部分領域を2つに繰返し分割することにより，積分推定値の要求された目標精度および目標確度に到達し，二分されたそれぞれについて積分と誤差推定を計算する．

NIntegrateの大域的適応型ストラテジーはMethodオプション値の"GlobalAdaptive"で指定できる：
オプション名
デフォルト値
MethodAutomatic各部分領域上の積分と誤差推定値を計算するために使われる積分則
"SingularityDepth"Automatic特異性ハンドラを適用する前の再帰的二分法の回数
"SingularityHandler"Automatic特異性ハンドラ
"SymbolicProcessing"Automatic記号的前処理を行う秒数

"GlobalAdaptive"オプション

"GlobalAdaptive"はNIntegrateのデフォルト積分ストラテジーである．これは一次元・多次元のどちらの積分に使うこともできる．"GlobalAdaptive"はデカルト積規則と完全対称多次元則で使うことができる．

"GlobalAdaptive"はヒープと呼ばれるデータ構造を使い，ヒープの最上部が最大の誤差領域となるようにして，領域の集合を部分的にソートした状態に保つ．アルゴリズムのメインループでは，最大誤差領域は，その誤差のほとんどの原因であると推定される次元で二分される．

このアルゴリズムは，ノードが領域となる二分木の葉を生成すると言うことができる．ノード・領域の子は二分法の後得られる部分領域である．

まず領域を二分してそれぞれの領域で積分を計算し，もとの領域上での大域的積分値と大域的誤差推定をそれぞれ，二分木の葉である各領域上で積分値の和および誤差推定の和として計算する．

それぞれの領域には，それが生成されるために次元について何回の二分法が行われたかが記録されている．領域の生成に行われた二分法が多すぎると，特異点平滑化アルゴリズムが適用される．特異点の処理を参照のこと．

"GlobalAdaptive"は，以下の式が真の場合に中止される．

ここでpgとagは目標精度と目標確度である．

このストラテジーは，1つの領域の再帰的二分法の数が一定数を超えた場合（MinRecursionとMaxRecursionを参照）あるいは大域的積分誤差の振動が大きすぎる場合（MaxErrorIncreasesを参照）にも中止される．

理論的および実践的な証拠から，大域的適応型ストラテジーは一般に局所的適応型ストラテジーよりもパフォーマンスが勝ると言える[MalcSimp75][KrUeb98]．

MinRecursionとMaxRecursion

再帰的二分法の最小および最大の深さは，オプションMinRecursionとMaxRecursionの値で指定する．

ある部分領域において，いずれかの次元の二分法の回数がMaxRecursionより大きくなると，"GlobalAdaptive"による積分は中止される．

MinRecursionを正の整数に指定することで，被積分関数が評価される前に積分領域の再帰的二分法を強制する．これは被積分関数の細く尖った部分を見逃さないようにするために行う（誤差推定器をごまかすを参照）．

多次元積分の場合は，MinRecursionの再帰の各レベルに対して各次元の二分法をできるだけ行おうとする．

"MaxErrorIncreases"

(2)は"GlobalAdaptive"で有効であると想定されるため，最大誤差領域の二分割およびその新しい領域上での積分後，大域的誤差は減少すると想定される．換言すると，大域的誤差は多かれ少なかれ，積分ステップの数に対して単調に減少すると予想される．

大域的誤差は，積分則の位相誤差のために振動することがある．それでも大域的誤差はある点で単調に減り始めるものと想定される．

以下はこの想定が誤りとなる場合である．

(i) 実際の積分がゼロになる．

ゼロ積分：

(ii) 指定された作業精度が，指定された目標精度に対して十分密ではない．

作業精度が十分密ではない：

(iii) 積分条件が悪い[KrUeb98]．例えば，被積分関数が複雑な式，または微分方程式や非線形代数方程式等の数学的問題の近似解で定義されている場合である．

"GlobalAdaptive"ストラテジーは，領域を最大の誤差推定値で二分した後に合計誤差推定が減少しなかった回数を記録している．その数が"GlobalAdaptive"のオプション"MaxErrorIncreases"を超えると，積分はメッセージ(NIntegrate::eincr)を出力して中止される．

"MaxErrorIncreases"のデフォルト値は一次元積分では400，多次元積分では2000である．

次の積分では"MaxErrorIncreases"のデフォルト値でメッセージNIntegrate::eincrが出力される：
"MaxErrorIncreases"を大きくするとメッセージNIntegrate::eincrは出力されなくなる：
結果は厳密値に匹敵する：

大域的適応型ストラテジーの実装例題

以下はガウス・クロンロッド分点，重み，誤差の重みを計算する：
これは，計算された分点と重みを持つ積分則を区間{a,b}上の関数 f に適用する関数の定義である：
区間{aArg,bArg}上で相対誤差 tol で関数 f の積分を見付ける単純大域的適応型アルゴリズムの定義である：
被積分関数を定義する：
前に定義した大域的適応型ストラテジーでは以下の結果となる：
これが厳密な結果である：
相対誤差は決められた許容誤差内である：

局所的適応型ストラテジー

積分推定値の要求精度および目標確度に達するために，局所的適応型ストラテジーは再帰的に部分領域をより小さい非隣接部分領域に分割し，それぞれに対する積分値と誤差推定値を計算する．

NIntegrateの局所的適用アルゴリズムはMethodオプション値"LocalAdaptive"で指定する：
オプション名
デフォルト値
MethodAutomatic部分領域上での積分値と誤差推定を計算するために使われる積分則
"SingularityDepth"Automatic特異点ハンドラを適用する前の再帰的二分法の回数
"SingularityHandler"Automatic特異点ハンドラ
"Partitioning"Automatic積分推定値を向上させるために領域を分割する方法
"InitialEstimateRelaxation"True不必要な計算を避けるための初期積分推定値の大きさを調整しようとする試み
"SymbolicProcessing"Automatic記号的前処理を実行する秒数

"LocalAdaptive"オプション

"GlobalAdaptive"と同様に，"LocalAdaptive"も一次元・多次元積分に使える．"LocalAdaptive"は直積型積分則と多次元の完全対称積分則の両方で使える．

"LocalAdaptive"ストラテジーは，初期化ルーチンとRR(再帰ルーチン)を持つ．RRは木の葉を生成し，そのノードが領域となる．ノード・領域の子がその分割により得られる部分領域である．RRは引数として領域を取り，それに対する積分値を返す．

RRは積分則を使い，領域引数の積分値および誤差推定値を計算する．誤差推定値が大きすぎる場合，RRは分割により得られた隣接しない部分領域に対して自身を呼び出す．これらの再帰的呼出しから返される積分値の総和は，領域の積分値になる．

RRは，それが実行される領域の積分値および誤差推定のみが分かると，再帰の継続を決定する（こういうわけで，このストラテジーは「局所的適応型」と呼ばれる）．

初期化ルーチンは，初期領域上の積分の初期推定値を計算する．この初期積分値はRRの中止基準で使用される．領域の誤差が初期積分値と比較して有意な場合，その領域は隣接しない領域に分割され，それに対してRRが呼ばれる．誤差が有意でなければ再帰は中止される．

領域の誤差推定値regionErrorは，

ならば有意でないと見られる．中止基準(3)は作業精度まで積分を計算する．積分値をユーザ指定の目標精度あるいは目標確度まで計算するために，次の中止基準が使われる．

ここでepsは作業精度において1+eps≠1となるような最小の数であり，pgとagはユーザ指定の目標精度および確度である．

"LocalAdaptive"の再帰的ルーチンは，次の場合に中止される．

1.  領域の境界線の間に指定された作業精度の数がない場合

2.  最大再帰レベルに到達した場合

3.  領域の誤差が有意でない，つまり基準(4)が真である場合

MinRecursionとMaxRecursion

"LocalAdaptive"のオプションMinRecursionとMaxRecursionは，"GlobalAdaptive"に対するものと同じ意味および機能を持つ．「MinRecursionとMaxRecursion」を参照のこと．

"InitialEstimateRelaxation"

最初の再帰が終了すると，よりよい積分推定値 が利用できるようになる．このよりよい推定値は，積分則で初期ステップに対する積分値()および誤差推定値()を与えるために使われた2つの積分推定値 ， と比較される．もし

ならば，(5)の積分推定値integralEstは数式

で増加させることができる—つまり，条件(6)は緩められる．それは が規則の積分推定値は規則の誤差推定値が予想するものよりも正確であるということを意味しているからである．

"Partitioning"

"LocalAdaptive"には，(7)を満足しない領域を分割する方法を指定するためのオプション"Partitioning"がある．一次元積分の場合，"Partitioning"がAutomaticに設定されていると，"LocalAdaptive"は再スケールされた積分則のサンプル点の間の領域を分割する．これで，積分則が閉形式ならば，すべての積分値が再利用できる．"Partitioning"に積分変数の数に等しい長さ の整数のリストが与えられると，積分領域の各次元 は 個の等しい部分に分割される．"Partitioning"に整数 が与えられると，すべての次元が 個の等しい部分に分割される．

以下の関数を考える：
これらは"LocalAdaptive"がその自動領域分割で使用するサンプル点である．画像から，各再帰レベルのサンプル点が前の再帰レベルのサンプル点の間にあることが分かる：
以下は，大きい誤差を持つ領域を3つの部分領域に分割する"LocalAdaptive"積分で使われるサンプル点である．形成されたパターンにより，第1および第2の再帰レベルの次の3つの再帰レベル部分領域がはっきり分かる：
"Partitioning"オプションを多次元に使った例である．プロットを生成するために，積分する最初の領域のサンプル点が取り除かれている：

被積分関数値の再利用

"LocalAdaptive"の一次元積分に対するデフォルトの分割設定では，(8)を満足しない積分値および誤差推定値を持つ部分区間の終端点における被積分関数値が再利用される．

"LocalAdaptive"による の積分のサンプル点である．変数rulePointsは"LocalAdaptive"で使用される積分則における点の数を決定する：
積分で再利用される点の百分率である：

局所的適応型ストラテジーの例題実装

以下でクレンショウ・カーチス則の分点，重み，誤差の重みを計算する：
これは，上で計算した分点および重みを持つ積分則を，区間{a,b}上で関数 f に適用する関数の定義である：
これは，相対誤差 tol で区間{aArg,bArg}における関数 f の積分値を求める，簡単な局所的適応型アルゴリズムの定義である：
関数を定義する：
局所的適応型ストラテジーが結果を与える：
厳密な結果である：
相対誤差は指定された許容誤差内である：

"GlobalAdaptive"と"LocalAdaptive"

一般に大域的適応型ストラテジーは，局所的適応型ストラテジーよりもパフォーマンスが優れている．しかし，局所的適応型ストラテジーの方がロバストでありパフォーマンスが優れている場合もある．

"GlobalAdaptive"と"LocalAdaptive"には2つの大きな違いがある．

1. "GlobalAdaptive"は全領域の誤差の総和が目標精度を満足すると終了する．一方"LocalAdaptive"は各領域の誤差が積分の推定に比べて十分小さいときに終了する．

2. 積分推定値を向上させるために，"GlobalAdaptive"は領域を最大誤差で二分するが，"LocalAdaptive"は十分小さくない誤差で全領域を分割する．

多次元積分の場合，"LocalAdaptive"は軸に沿って分割を実行するため，領域の数は組合せ論的に増加する可能性がある．したがって，"GlobalAdaptive"の方がずっと速い．

大域的適応型ストラテジーの方が一次元の滑らかな被積分関数に対してなぜどのように速いのかは[MalcSimp75]で証明（説明）されている．

"LocalAdaptive"の方が"GlobalAdaptive"より速くパフォーマンスも優れている場合，それは"LocalAdaptive"の目標精度中止基準および分割ストラテジーの方が被積分関数の特性に適しているからである．別の要因は，"LocalAdaptive"がすでにサンプリングされたすべての点の積分値を再利用できるということにある．"GlobalAdaptive"はほんのわずかな積分値しか再利用できない（規則の適用につき最大で3つ，一次元積分のデフォルトであるガウス・クロンロッド則では0）．

次では，"GlobalAdaptive"と"LocalAdaptive"のパフォーマンスの差を示す．

通常"LocalAdaptive"に勝る"GlobalAdaptive"

所要時間の比と被積分関数評価の数を含む下の表は，ほとんどの場合"GlobalAdaptive"の方が"LocalAdaptive"よりもよいことを示している．考慮されるすべての積分は上の一次元積分である．なぜならば，(i) "LocalAdaptive"は各軸に沿って領域を分割するため，多次元積分ではパフォーマンスの差は深くなることが予想されるからであり，(ii) 異なる範囲上の一次元積分は上になるよう再スケールすることができるからである．

以下は関数，目標精度，積分回数，積分則の定義である．変数integrationRuleは，同じ積分則でプロファイル実行を行うために変更することができる．最後の関数はをに変換する変数の変更 により から導出されている：
厳密な積分値．すべての積分は上である：
"GlobalAdaptive"の所要時間：
"LocalAdaptive"の所要時間：
"GlobalAdaptive"関数の評価：
"LocalAdaptive"関数の評価：
時間の比と被積分関数の評価の表：
積分の誤差の表である．"GlobalAdaptive"と"LocalAdaptive"の両方が必要とされる目標精度に到達している：

特異点の処理

NIntegrateの適応型ストラテジーにより，積分領域境界線およびユーザ指定の特異点または多様体における変数変換を介した収束がスピードアップされている．適応型ストラテジーは，特異点における被積分関数の評価結果も無視する．

特異点の指定は「ユーザ指定の特異点」で説明する．

変数変換で多次元の特異点を扱う場合は注意が必要である．「IMT多次元特異点処理」を参照するとよい．多次元積分に対する座標変換により特異点を簡約あるいは削除することができる．「多次元特異点処理のためのDuffyの座標」を参照のこと．

NIntegrateがどのように特異点を無視するかの詳細は「特異点の無視」に記述してある．

コーシー主値積分の計算は「コーシー主値積分」に記述してある．

ユーザ指定の特異点

点の特異性

特異点が発生した場所が分かっていると，それは積分範囲あるいはオプションExclusionsで指定することができる．

およびにおける2つの特異点を持つ積分の例である：
における特異点を持つ二次元積分の例である：
およびにおける2つの特異点をExclusionsオプションで指定した積分の例である：
における特異点をExclusionsオプションで指定した二次元積分の例である：
曲線，曲面，超曲面の特異点

一般に曲線，曲面，超曲面上の特異点は，方程式のオプションExclusionsで指定することができる．このような特異点は通常変数範囲を使っては指定できない．

以下の二次元関数は曲線 に沿って特異である：
Exclusionsを使うと，積分はすぐに計算される：
特異点の指定が与えられていないと，NIntegrateはずっと遅く収束する：
以下は特異曲線が変数範囲で指定できる場合の例である．もし かつ であれば，これは不可能である．以下の例を参照のこと：
曲線，曲面，超曲面の特異点処理の例題実装

特異点が生じている曲線，曲面，超曲面が暗示的形式（1つの方程式として記述できる）で分かっている場合，関数Booleを使って特異曲線，曲面，超曲面を境界として持つ積分領域を形成することができる．

以下の二次元関数には曲線 に沿って特異点がある：
Booleを使うと，積分は速く計算される：
以下の二次元関数には曲線 に沿って特異点がある：
ここでまたBooleを使うと，積分が速く計算される：
積分のサンプル点はこのように見える：
以下の関数は特異曲線，曲面，超曲面の指定を取り，関数Booleを使って境界線上に特異点を持つ積分領域を作成する：
以下で三次元関数を定義する：
曲面 に沿って特異点を持つ三次元関数の積分である．
積分のサンプル点である：

"SingularityHandler"と"SingularityDepth"

適応型ストラテジーは領域の二分により積分推定値を向上させる．適応型ストラテジーの部分領域がオプション"SingularityDepth"により指定された二分法の数により得られるならば，その部分領域には特異点があると決まる．その部分領域上の積分は"SingularityHandler"により指定された特異点ハンドラで行われる．

オプション名
デフォルト値
"SingularityDepth"Automatic特異点ハンドラを適用する前の再帰的二分法の数
"SingularityHandler"Automatic特異点ハンドラ

"GlobalAdaptive"と"LocalAdaptive"の特異点ハンドラオプション

指定された積分領域の境界上に積分可能な特異点がある場合，収束が起る前はMaxRecursionまで簡単に二分法が繰り返される．この状況に対処するために，NIntegrateの適応型ストラテジーは変数変換(IMT，"DoubleExponential"，SidiSin）を使い，積分収束あるいは特異点の次数を緩める領域変換（Duffyの座標）を高速化する．変数変換特異点ハンドラの理論的背景はオイラー・マクローリンの公式[DavRab84]に記載されている．

IMT変数変換の使用

IMT変数変換は，文献ではIMT公式[DavRab84][IriMorTak70]と呼ばれる，伊理・森口・高沢により提唱された求積法の変数変換である．IMT公式は，新しい被積分関数のすべての導関数が積分区間の終点で消失するように，独立変数を変換すると言う考えに基づいている．その後，台形則が新しい被積分関数に適用され，適切な条件下で確度の高い結果が達成される[IriMorTak70][Mori74]．

以下は特異点処理に対するIMT変数変換を使用する数値積分である：
オプション名
デフォルト値
"TuningParameters"10IMT変換公式 の調整パラメータである数値のペア{a,p}．1つの数 a のみが与えられた場合，それは{a,1}と解釈される

IMT特異点処理ハンドラのオプション

NIntegrateの適応型ストラテジーではIMT変換だけを使用する．領域に特異点があると決まると，その被積分関数にIMT変換が適用される．積分は台形則ではなく，変換前に使われていたのと同じ規則で続行する（"DoubleExponential"を使った特異点処理では台形積分則に切換えられる）．

また，NIntegrateの適応型ストラテジーでは，変換された被積分関数がどちらか一方の端で消失する，もとのIMT変換の変形が使われる．

IMT変換 ()を定義する：

パラメータ a と p は調整パラメータと呼ばれる[MurIri82]．

IMT変換の導関数の極限はである：
以下はIMT変換のプロットである：

上のグラフから，変換されたサンプル点は0付近の方がずっと密であることが分かる．これは，被積分関数が0において特異であれば，より効率よく抽出されることを意味する．それは積分則サンプル点の大部分は，大きい被積分関数値を積分則の積分推定値に起因させるためである．

任意の指定された作業精度について，付近の数は付近の数よりもずっと密であるため，領域を二分した後でNIntegrateの適応型ストラテジーは二分された区間の右端を含む部分領域の二分変数を入れ換える．これは次のプロットで見ることができる：

IMT変数変換が適用される領域の部分領域に適用される特異点ハンドラは他にはない．

IMT変換の例

で特異値を持つ，区間上の関数を考えてみる：
特異点ハンドラIMTと特異点の深さを使い，"GlobalAdaptive"で積分を実行するとする．4回二分すると，"GlobalAdaptive"は特異な終点を含む境界の領域を持つ．その領域について，IMT変数変換はその境界をに，被積分関数を下のように変更する：
以下は新しい被積分関数のプロットである：

特異点が破壊されている．

しかしサンプル点のいくつかが特異な終点に近付きすぎているので，IMT変換により特異点と一致しているサンプル点には特に注意が必要である．NIntegrateは特異点における評価を無視する．詳細は「特異点の無視」を参照のこと．

ガウス・クロンロッド則のサンプル点と重みを考えてみる：
領域に対するガウス・クロンロッドサンプル点および再スケールの導関数は次である：
これは積分推定値である：
IMT変換を使うと，これらはサンプル点と導関数である：
IMT変換を使った積分推定値である：
IMT変数変換を使って計算した推定値は，厳密値にずっと近い：

二重指数関数型公式の使用

適応型ストラテジーでIMT変数変換が使用される場合，IMT変換された領域の積分則は変更されない．これとは対照的に，特異点を持つと想定されている領域に対して変数変換と異なる積分則の両方を使うことができる（これはIMT公式の姿勢である[DavRab84]）．まったくそのようなことが二重指数関数型公式（二重指数関数型公式で台形則）が使用されたときに起る．

NIntegrateは一次元積分に対してのみ，特異点処理のために二重指数関数型公式を使うことができる．

以下は特異点処理のための二重指数関数型公式を使う数値積分である：

一次元積分でのIMTと"DoubleExponential"と非特異点処理

どちらの特異点ハンドラ（IMTと"DoubleExponential"）も多すぎる二分回数（"SingularityDepth"で指定されたように）で得られた領域に適用される．

その2つの主な違いは，IMTは適用される領域の積分推定値を計算するために使われる積分則を変更しないと言うことである．IMTは変数変換に過ぎない．一方，"DoubleExponential"は変数変換および異なる積分則（台形則）の両方を使い，適用される領域上の積分推定値を計算する．換言すると，特異点ハンドラの"DoubleExponential"は二重指数関数型ストラテジーで説明してあるように，二重指数関数型公式に積分を委託する．

その結果，IMT特異点ハンドラが適用される領域は，まだ適応型積分ストラテジーによる二分法の対象となる．ゆえに，目標精度に到達するまで，最後の二分法の前に実行された被積分関数の評価は捨てられる．一方，"DoubleExponential"特異点ハンドラが適用される領域は二分されない．"DoubleExponential"で使用される台形則は，各ステップでサンプル点が増加する領域上の積分推定値を計算し，前のステップからのサンプル点の被積分関数評価を完全に再利用する．

したがって，被積分関数が，終点が特異点である領域上で「非常に」解析的である（被積分関数および積分変数に関して導関数に急速あるいは突然の変化がない）場合，"DoubleExponential"特異点ハンドラはIMT特異点ハンドラよりもずっと速くなる．被積分関数が"DoubleExponential"特異点ハンドラに与えられた領域において解析的でない，あるいは被積分関数の二重変換の収束が遅すぎるという場合は，IMT特異点ハンドラに切り換えた方がよい．この切換えはオプション"SingularityHandler"をAutomaticに設定して行う．

以下の表では，異なる二分の深さにおいて適用されたIMT，"DoubleExponential"，Automaticの特異点ハンドラを比較する．

以下で，数値積分コマンドで必要とされるサンプル点の数と時間を与えるプロファイル関数NIntegrateProfileを定義するパッケージをロードする：
"DoubleExponential"特異点ハンドラで簡単に計算できる「非常に」解析的な被積分関数に対する表：
特異点を持たずほぼ非連続な導関数を持つ被積分関数（あまり解析的ではない）に対する表．Automatic特異点ハンドラは"DoubleExponential"から始まり，IMTに切り換えられる：
Automatic特異点ハンドラが"DoubleExponential"から始まりIMTに切り換わるような被積分関数に対する表：

IMT多次元特異点処理

IMT特異点ハンドラを多次元積分に使うと，特異点が軸のいずれかに沿っている場合だけ積分過程がスピードアップする．特異点が積分領域の角にある場合は，IMTを使うことは逆効果である．先に定義した関数NIntegrateProfileを次の例で使う．

軸だけに沿った特異点を持つ被積分関数に対する評価回数と時間である．デフォルトの自動特異点ハンドラは，デフォルトで4回二分した後得られた領域にIMTを適用することを選択する：
だけに沿った特異点を持つ被積分関数に対する評価回数と時間である．特異点ハンドラは適用されない：
積分領域の角に特異点を持つ被積分関数に対する積分評価回数と時間である．デフォルト（自動）の特異点ハンドラは，デフォルトで4回二分した後得られた領域に，特異点ハンドラDuffyCoordinatesを適用することを選択する：
積分領域の角に特異点を持つ被積分関数の被積分評価の数と時間である．デフォルトで4回二分した後得られた領域にIMTが適用される：
積分領域の角に特異点を持つ被積分関数に対する被積分評価の回数と時間．特異点ハンドラは適用されない：

多次元特異点処理のためのDuffyの座標

Duffyの座標は，いずれかの角に特異点を持つ正方形，立方体，超立方体上の被積分関数を線上の特異点を持つ被積分関数に変換する方法である．後者の方が積分しやすい場合がある．

以下の積分ではDuffyの座標が使ってある：
以下の積分にはDuffyの座標は使っていない：

NIntegrateのストラテジーである"GlobalAdaptive"と"LocalAdaptive"は積分領域の角だけでDuffyの座標を適用する．

ある点で多次元積分の特異点が発生すると，変数の結合により一次元積分で使用される特異点変数変換が逆効果になる．[Duffy82]でDuffyにより提唱された幾何学的性質を持つ変数変換は，積分領域の角にある特異点を，平面上の「柔らかい」特異点で置き換える変数の変更を行う．

が積分の次元で ならば，Duffyの座標は次のタイプの特異点に適したものである（再び[Duffy82]を参照）．

1.  , , ;

2.  , , ;

3.  , , ,

例えば，以下の積分

を考えてみる．積分領域が規則 でに変更されると，そのヤコビアンは で積分は以下のようになる．

最後の積分にはまったく特異点がない．

また，次の積分を考えてみる．

これは総和

に等しい．この総和の第1積分は(9)のように変換される．しかし，2つ目は によるのへの変更にヤコビアン を持つ．これは項の打消しをもたらさない．積分の順序を変えてみる．

これだと第2積分は(10)の変換に従う．

（方程式(3)の第2積分では，変数は置換される．これは数学的等価性を証明するために必要ではないが，積分を計算するときに速い．）

積分(11)は特異点のない積分として書き換えることができる．

積分変数が(12)で置換されないならば，積分(13)は以下のように書き換えられる．

これは，その被積分関数が単純にどちらの軸にも沿っていないので，より複雑な積分である．その結果前のものよりも計算が難しい．

より簡単な積分に対するサンプル点の数である：
より複雑な積分に対するサンプル点の数である：

NIntegrateは上の例で任意次元の手法の一般化を使っている（[Duffy82]では三次元が記述されているだけである）．一般化記述との例題実装を下に挙げる．

に対する異なる特異点処理方法を比較する表である（先で定義したプロファイル関数NIntegrateProfileを使う）：

Duffyの座標ストラテジー

Duffyの座標が適用できる場合，実際の積分が始まる前にDuffyの座標の変化が起ると，数値積分の結果が速く得られる．しかし事前に変換を行うには，積分領域のどの角で特異点が発生するかが分かっていなければならない．NIntegrateの"DuffyCoordinates"ストラテジーはそのような事前積分変換を簡単にする．

積分領域の異なる2つの角に特異点を持つ被積分関数の例である：
オプション名
デフォルト値
Method{"GlobalAdaptive","SingularityDepth"->∞}Duffyの座標変換を適用した後に積分を行うストラテジー
"Corners"AllDuffyの座標変換を適用する角を指定するベクトルあるいはベクトルのリスト．ベクトルの要素は0か1である．各ベクトルの長さは積分の次元に等しい

"DuffyCoordinates"オプション

"DuffyCoordinates"がまず行うのは，積分を単位超立方体（あるいは正方形か立方体）上にある積分に再スケールすることである．1つの角だけが指定されている場合，"DuffyCoordinates"は上で記述してあるようにDuffyの座標変換を適用する．2つ以上の角が指定してある場合は，前のステップの単位超立方体が，辺が1/2である隣接しない立方体に分割される．これらの隣接しない立方体上の積分を考えて見る．Duffyの座標変換は特異となるよう指定された頂点を持つ立方体に適用される．残りは単位立方体上の積分へと変換される．この時点ですべての積分は単位立方体である積分領域を持つので，それらは加算されその和は"DuffyCoordinates"に与えられるのと同じオプションであるMethodオプションを持つNIntegrateに与えられる．

"DuffyCoordinates"で使われる実際の積分は，NIntegrateと同じ引数を取るNIntegrate`DuffyCoordinatesIntegrandで得ることができる．

以下は積分領域の1つの角で特異となる三次元関数の"DuffyCoordinates"被積分関数の例である：
以下は積分領域の2つの角で特異となる二次元関数の"DuffyCoordinates"被積分関数の例である：

"DuffyCoordinates"は，「多次元特異点処理のためのDuffyの座標」に記述してある被積分関数のタイプで顕著なスピードの向上を引き起こすことがある．

"DuffyCoordinates"を使った積分：
前の例よりもずっと遅いデフォルトのNIntegrateオプション設定を使った例：
"DuffyCoordinates"による別のスピードアップの例：
上の例よりもずっと遅いデフォルトのNIntegrateオプション設定の例：

Duffyの座標の一般化と例題実装

Duffyの座標の理論については，「多次元特異点処理のためのDuffyの座標」を参照のこと．

実装は以下の2つの定理に基づく．

定理 1： 次元の立方体は幾何学的に等価な 個の互いに素な 次元角錐（規定が次元立方体で頂点が一致）に分割される．

証明：立方体の辺の長さがで，立方体が原点に頂点を持ち，他のすべての頂点の座標がかであるとする．次元の立方体の壁 （ここで ）を考える．その数は厳密に であり，原点はそれに入っていない．個の壁のそれぞれは原点を持つ角錐を形成する．これで定理は証明される．

次は定理を3Dで示したプロットである：

本の軸が と表される場合，壁 で形成された角錐がと記述できるとする．を循環的に 回左に回転させた（つまりRotateLeftをに 回適用した）後に導出される置換を で表す．すると次の定理が成り立つ．

定理 2：単位立方体上の任意の積分で，次の等式が成り立つ．

証明：最初の等式は定理1に従う．2つ目の等式は角錐を立方体に変換する変数の変化だけである．

以下は指定された辺を領域に入れる超立方体の変換に対する規則およびヤコビアンを与える関数である：
単位平方の無限領域再スケールの例である：
特異点が原点であるときに，Duffyの座標により得られる積分を計算する関数である：
以下は，特異点が生じる超立方体の指定された角に対するDuffyの座標法により得られた積分を計算する関数である：
記号的な例である：
別の記号的な例：
計算例である：
Duffyの座標を使った方が，特異点処理しないよりもずっと速い（次の例を参照）：
特異点処理を使わない積分．
もちろんNIntegrateの内部実装で同様のパフォーマンスの結果が得られる：

特異点の無視

特異点処理の別の方法に，無視するということがある．NIntegrateは特異点と一致するサンプル点を無視する．

1において特異点を持つ次の積分を考える．

積分変数が1に近いとき，被積分関数はになる．

次は被積分関数のプロットである：
NIntegrateは厳密な結果に近い結果を与える：
MaxRecursionが増加すると収束が達成される：

以下で分かるように，NIntegrateはデフォルトオプションでは1でサンプル点を持つ．

NIntegrateがサンプル点として1を持つことをチェックする：

しかしNIntegrate[Log[(1-x)2],{x,0,2}]では，評価モニタは1であるサンプル点を選んでいない．

区間に属するサンプル点：

換言すると，1における特異点は無視される．特異点を無視することは特異なサンプル点でゼロである被積分関数を持つことに等しい．

特異点が変数範囲で指定されるならば，積分は簡単に積分される．次は，特異および非特異な範囲指定のNIntegrateに対するサンプル点の数と所要時間である．

特異点を指定した積分：
特異点を無視することによる積分：

特異点を無視することのもっと面白い例は，被積分関数の分母にベッセル関数を使ったものである．

いくつか（5つ）の積分可能特異点を持つ積分：

結果はBesselJ[2,x]の零点を持つ特異点範囲指定のNIntegrateを使って検証することができる（BesselJZeroを参照）．

ベッセルの零点が特異点として指定された積分：

言うまでもなく，最後の積分にはBesselJの零点の計算が必要であった．前者は全く被積分関数を解析しないでただ積分するだけである．

特異点を無視することは振動する被積分関数では有効でないかもしれない．

例えば，以下の2つの積分は等価である：
NIntegrateは最初の積分が実行できる：
NIntegrateは2つ目は実行できない：

しかしながら，被積分関数がその特異点の近傍において単調ならば，つまり単調な積分可能関数によりマジョライズされるならば，特異点を無視することにより収束が達成できることを示すことができる．

特異点を無視することの理論的正当性と実践的な推薦は[DavRab65IS]および[DavRab84]を参照のこと．

自動特異点処理

一次元積分

オプション"SingularityHandler"が一次元積分に対してAutomaticに設定されている場合，分割の"SingularityDepth"の数により得られる領域には"DoubleExponential"が使われる．前述の通り，"DoubleExponential"特異点ハンドラがこの領域に対して動作する限り，領域はそれ以上分割されない．"DoubleExponential"により計算される誤差推定値が二重指数関数型公式の理論により予言されるように進化しないならば，この領域に対する特異点処理はIMTに切り換えられる．

「収束率」で述べているように，次の誤差の依存性は二重指数関数的サンプル点の数について予想される．

ここで は正の定数である．それぞれ 個と 個（ここで ）の数のサンプル点で作成された，2つの連続した二重指数関数型公式の計算の相対誤差 と を考える．，， と仮定すると，以下が想定される．

"DoubleExponential"からIMTへの切換えは，以下の場合に起る．

(i) 領域の誤差推定が領域の積分推定値の絶対値よりも大きい（よって相対誤差はより小さくない）

(ii) 不等式(2)が2つの異なる場合で真ではない

(iii) 二重指数関数型変換で計算された被積分関数の値がゆっくりとしか崩壊しない．

次は"DoubleExponential"からIMTへの特異点ハンドラの切換えの例である．プロット上で，被積分関数は y 軸の順に x 軸でサンプルされている．上のサンプル点のパターンはガウス積分法()から二重指数関数型公式()への切り換えを示しており，これは後でIMT変数変換()を使ってガウス積分法により置き換えられる：
多次元積分

多次元積分でオプション"SingularityHandler"がAutomaticに設定されていると，"DuffyCoordinates"とIMTの両方が使われる．

"DuffyCoordinates"を適用するためには，領域は次の条件に合っていなければならない．

領域は各軸に沿った"SingularityDepth"数の二分（分割）で得られたものである

領域は初期積分領域の中のひとつの角である（指定された積分領域は，区分処理あるいはユーザ指定の特異点により積分領域に分割することができる）

IMTを適用するためには，領域は次の条件に合っていなければならない．

領域は，主に1つの軸に沿った"SingularityDepth"数の二分（分割）で得られたものである

領域は角の領域ではなく，初期積分領域のうちの1つの辺上にあるものである

換言すると，IMTは"SingularityDepth"数の分割で得られたが"DuffyCoordinates"自動適用の条件は満足しない領域に適用される．

IMTは，特異点がいずれかの軸に沿っている場合に効率的である．点の特異性に対してIMTを使うのは逆効果になり得る．

二次元積分 のサンプル点にAutomatic（左）と"DuffyCoordinates"（右）の特異点処理を施す．自動特異点処理では"DuffyCoordinates"のほぼ2倍の点が使われるのが分かる．特異点ハンドラの効果を例示するために，2回二分した後にハンドラを適用する：
積分 の所要時間を，特異点ハンドラAutomatic，"DuffyCoordinates"，IMT，ハンドラなしの場合で比較する．積分はで点の特異性を持つ：
軸に沿って特異な積分 の所要時間を，特異点ハンドラAutomatic，"DuffyCoordinates"，IMT，ハンドラなしの場合で比較する：

コーシーの主値積分

積分のコーシーの主値を評価するために，NIntegrateではストラテジーPrincipalValueが使われる．

2において特異点を持つコーシーの主値積分である：

NIntegrateのPrincipalValueでは，難しさのない領域を直接操作するためにMethodオプションで指定されたストラテジーが使われる．また，正・負の値の打消しを利用するためには，指定された特異点付近で値を対称に対にすることにより指定されたストラテジーが使われる．

オプション名
デフォルト値
MethodAutomatic部分領域上の推定値を計算するために使われるメソッドの指定
SingularPointIntegrationRadiusAutomatic数ϵ1 あるいは，範囲指定の中の特異点 , , …, に対応する数のリスト{ϵ1,ϵ2,…,ϵn}．各ペアで形式 の積分が形成される

"PrincipalValue"オプション

したがって，指定

は

として評価される．ここでそれぞれの積分はMethod->methodspec としたNIntegrateを使って評価される．もしϵ が明示的に指定されていないならば，値は b-a と c-b の差分に基づいて選ばれる．オプションSingularPointIntegrationRadiusは特異点の数に等しい数のリストを取ることができる．公式の導出については[DavRab84]を参照のこと．

のコーシーの主値を見付ける：
のコーシーの主値である．指定しなければならない特異点が2つある：
特異点はExclusionsオプションを使って指定することができる：
これで値を検証する．すべて厳密に行われたら結果は0になる：

特異点は厳密に見付けなければならない．アルゴリズムは特異点の両側の点を対にするので，特異点の位置が少しでも異なると，極付近の相殺がうまくいかず，NIntegrateが収束しても結果は誤ったものとなり得る．

サンプル点の可視化

以下の主値の計算を考える．

下の例では，サンプル点の可視化の方法を2つ示す．最初は使用されるサンプル点を示す．被積分関数は主値積分を実行するために変更しなければならないので，もとの被積分関数が評価される点を見た方がよいかもしれない．これは2つ目の例で示す．

以下はNIntegrateで使用されるサンプル点である．区間にはPrincipalValueの積分 のためにサンプル点はないが，にはサンプル点がある：
これは被積分関数に与えられる引数値を累積する関数を定義する：
ここには被積分関数が評価された点がある．区間上の対称性に注目のこと：

二重指数関数型ストラテジー

二重指数関数型公式は変数変換の後に台形則を適用することからなる．二重指数関数型公式は1974年に森・高橋により提唱されたもので，いわゆるIMT公式およびTANH規則からアイディアを得たものである．この変換には「二重指数関数型」という名前が付いているが，これは被積分関数の変数が積分領域の最後に達すると，その導関数が二重関数的に減少するためである．

NIntegrateの二重指数関数型アルゴリズムはMethodオプション値"DoubleExponential"で指定される：
オプション名
デフォルト値
"ExtraPrecision"50内部的に使用される最大追加精度
"SymbolicProcessing"Automatic記号的前処理を実行する秒数

"DoubleExponential"オプション

二重指数関数型ストラテジーは，一次元積分にも多次元積分にも使える．多次元積分に適用されたときは，台形則のデカルト積が使われる．

二重指数関数型変換 では，積分

が

に変換される．ここでは有限，半無限()，無限()のどれでもよい．被積分関数 はにおいて解析的でなければならず，1つあるいは両方の終点で特異点を持つことがある．

変換された被積分関数は二重関数的に減少する．つまりに近付くにつれ， となるのである．

関数 はにおいて解析的である．解析的被積分関数の(14)のような積分では，台形則が最適な規則であることが知られている[Mori74]．

異なるタイプの積分領域に対して使われる変換には

があり， および は有限数である．

台形則は(15)に適用される．

(16)の項は，十分大きいのときに二重指数関数的に衰退する．したがって，(17)の和は，総和に関与しないほど小さい項で切り取られる（局所的適応型ストラテジーでは(18)に類似した基準が使われる．次の「二重指数関数型積分法の例題実装」も参照のこと）．

ストラテジー"DoubleExponential"では二重指数関数型公式が使われる．

"DoubleExponential"ストラテジーは解析的な被積分関数に最も効果的である．「二重指数関数型積分法とガウス積分法との比較」を参照のこと．

"DoubleExponential"では多重積分に二重指数関数型公式の直積が使われる．

二重指数関数型公式の直積：

他の直積型公式でそうであるように，"DoubleExponential"が3より大きい次元に使われると，組合せ的爆発により非常に遅くなる可能性がある．

次のプロットは"DoubleExponential"多次元積分のデカルト積記号を例示する：

二重指数関数型公式は適応型ストラテジーの特異点処理に使うことができる．詳細は「特異点処理」に記述してある．

MinRecursionとMaxRecursion

オプションMinRecursionは「MinRecursionとMaxRecursion」で記述してある"GlobalAdaptive"および"LocalAdaptive"に対して持つのと同じ意味と機能を持つ．"DoubleExponential"のMaxRecursionは台形求積推定値が向上する回数を制限する．詳細は「二重指数関数型積分法の例題実装」を参照のこと．

二重指数関数型積分法とガウス積分法との比較

"DoubleExponential"ストラテジーは解析的な被積分関数に最も効果的である．例えば，以下の積分はガウス積分法（大域的適応型アルゴリズムを使う）よりも"DoubleExponential"で実行した方が3倍速い．

"DoubleExponential"を使った積分：
ガウス積分法を使った積分（NIntegrateのデフォルトストラテジーである"GlobalAdaptive"では，デフォルトでつのガウス点とつのクロンロッド点のガウス・クロンロッド積分則が使われる）：

"DoubleExponential"は評価点の数に関して二重関数的に収束するので，目標精度を上げても"DoubleExponential"であまり効果が得られない．これを2つの積分 と で説明する．それぞれの表には誤差と評価回数が示してある．

に対する二重指数関数型積分法とガウス積分法である．目標精度を上げても"DoubleExponential"で使用されるサンプル点の数は変化しない：
に対する二重指数関数型積分法とガウス積分法である．目標精度を上げても"DoubleExponential"で使用されるサンプル点の数は変化しない（積分は記号的前処理なしで実行される）：

一方，非解析的な被積分関数では"DoubleExponential"は非常に遅く，ガウス積分法を使う大域的適応型アルゴリズムは簡単に特異点を解決することができる．

"DoubleExponential"では，非解析的な被積分関数でこの積分を計算するのに，1万回以上の被積分関数の評価が必要である：
この積分には，ガウス積分法の方がずっと速い：

さらに，"DoubleExponential"はほぼ非連続な導関数を持つ被積分関数，つまりあまり解析的でない被積分関数により遅くなる場合がある．

あまり解析的でない被積分関数の例である：
ここでもガウス積分法の方がずっと速い：
被積分関数とその導関数のプロットである：

収束率

このセクションでは，使用される評価点の数 について二重指数関数型公式の漸近誤差が

であることを示す． は正の定数である．

これで積分推定値と使用される点の数を返す二重指数関数型積分関数を定義する：
関数を定義する：
厳密な積分である：
以下は，台形則の刻み幅の範囲に対する誤差および評価点の数を見付ける：
これは誤差の対数を通してにフィットする．(19)を参照のこと：
フィットした関数である．総和項30.48は翻訳パラメータである：
誤差がモデル(20)にフィットするのが分かる：

二重指数関数型積分法の例題実装

次に挙げるのは，有限領域変数変換の二重指数関数型積分法の例題実装である（上の変換(21)）.

次は台形則を，変換された被積分関数に適用する関数の定義である.この関数は(22)を使い，2倍大きいステップで計算される積分推定値を再使用するよう強制される：
次は簡単な二重指数関数型ストラテジーの定義である．これは相対誤差 tol で有限区間{a,b}上の関数 f の積分を見付ける：
で特異となる関数を定義する：
以下は二重指数関数型ストラテジーからの積分推定値である：
以下が厳密な結果である：

2つの結果は同じである．

次は振動関数を定義する：
二重指数関数型ストラテジーにより与えられる積分推定値である：
厳密な結果である：
次は機械精度での厳密な結果である：
相対誤差は設定された許容誤差内にある：

"Trapezoidal"ストラテジー

"Trapezoidal"ストラテジーは，積分区間が厳密に1周期である場合に，解析的な周期的被積分関数に最適な収束を与える．

オプション名
デフォルト値
"ExtraPrecision"50内部的に使用される最大の追加精度
"SymbolicProcessing"Automatic記号的前処理を実行する秒数

"Trapezoidal"オプション

"Trapezoidal"は"DoubleExponential"と同じオプションを取る．積分範囲が無限あるいは半無限の場合，"Trapezoidal"は"DoubleExponential"になる．

（台形則での）周期関数積分の理論的背景，例題，説明は[Weideman2002]を参照のこと．

積分 に対して"GlobalAdaptive"と"Trapezoidal"のそれぞれで使用されるパラメータ の異なる値に対するサンプル点の数を示す表である：
例題の実装
この関数は，指定された点を使って台形則の積分推定値を作成する：
以下の関数は，古いサンプル点の間のサンプル点を使い，台形則の積分推定値を向上させる：
この関数は先行する関数のインターフェースである：
ベッセル関数の定義である：
台形則の推定値である：
厳密値である：
相対誤差は，指定された許容誤差内にある：

振動ストラテジー

NIntegrateには振動積分のためのメソッドがいくつか含まれている．一次元および多次元の振動積分という大きいクラスには，積分則"LevinRule"が適用されれる．これは"GlobalAdaptive"等の適応型規則ベースのストラテジーとともに使われる．

NIntegrateにはある種の一次元振動積分に特化された積分ストラテジーもいくつか含まれている．通常，これらのアルゴリズムは，有限区間の積分か無限区間の積分のみに使われる．有限区間上の振動積分の場合，NIntegrateは被積分関数のチェビシェフ(Chebyshev)展開と大域的適応型積分ストラテジーを使う．無料区感上の振動積分の場合は，NIntegrateは修正二重指数アルゴリズム，あるいは被積分関数の零点間の区間上にある積分列での列総和加速を使う．

次の例では，異なる部分区間に対してそれぞれ特化された振動ストラテジーがすべて使われている：

NIntegrateは自動的に振動（一次元）被積分関数を検出し，被積分関数の範囲に従ってどのストラテジーや規則を使えばよいか，また特定の振動形式を選ぶ．

ここで説明してある特化されたストラテジーにより扱われる積分は，以下の形式である．

ここで振動カーネル は以下の形式を取る．

1.  有限のときは ，，

2.  無限あるいは半無限のときは ，，，，，，，，

これらの振動カーネル形式で，，， は実定数， は正の整数である．

その積分則で扱われる振動被積分関数のより一般的な形式の説明は，"LevinRule"を参照されたい．

有限領域振動積分

変形クレンショウ・カーチス則([PiesBrand75][PiesBrand84])は以下の形式

の有限領域一次元積分公式である．ここで ，，，， は有限実数である．

変形クレンショウ・カーチス則はチェビシェフ多項式展開により1つの多項式で を近似する．これにより，計算が簡約化される．正弦関数および余弦関数を持つチェビシェフ多項式は直交であるためである．変形クレンショウ・カーチス則はストラテジー"GlobalAdaptive"で使われる．滑らかな では，変形クレンショウ・カーチス則は通常振動積分に対する他のアプローチ（Filonの求積法や被積分関数の零点間のマルチパネル積分）よりも優れている[KrUeb98]．

変形クレンショウ・カーチス則は形式(1)の高度に振動する積分に非常に適している．例えば，変形クレンショウ・カーチス則ではとの両方に対して使われる被積分関数の評価が100に満たない．

ゆっくりと振動するカーネルに対する変形クレンショウ・カーチス則での被積分関数の評価回数：
ゆっくりと振動するカーネルに対する変形クレンショウ・カーチス則での所要時間と積分推定値：
激しく振動するカーネルに対する変形クレンショウ・カーチス則での被積分関数の評価回数：
激しく振動するカーネルに対する変形クレンショウ・カーチス則での所要時間と積分推定値：

一方，記号的前処理をしないと，デフォルトのNIntegrateメソッドであるガウス・クロンロッド則の"GlobalAdaptive"ストラテジーは，に対して何千もの評価を使い，は積分することができない．

ゆっくりと振動するカーネルに対するガウス求積法での被積分関数の評価回数：
ゆっくりと振動するカーネルに対するガウス求積法での時間と積分推定値：
高度に振動するカーネルに対するガウス求積法での被積分関数の評価回数：
高度に振動するカーネルに対するガウス求積法での時間と積分推定値：

外挿振動ストラテジー

NIntegrateの"ExtrapolatingOscillatory"ストラテジーは無限の一次元領域の振動積分に対するものである．このストラテジーは被積分関数の2つの連続する零点間の領域を持つ積分のそれぞれから構成される数列の総和に対して数列の収束加速法を使用する．

"ExtrapolatingOscillatory"を使った積分の例：
オプション名
デフォルト値
MethodGlobalAdaptive零点間の積分をするために使われる積分ストラテジーであり，ExtrapolatingOscillatoryが失敗したときに使われる
"SymbolicProcessing"Automatic記号的処理を実行する秒数

以下の積分

を考える．関数 は振動カーネルであり，関数 は滑らかである． を積分の下限（有限）から列挙された の零点であるとする．つまり，不等式 が成り立つということである．もし積分(23)が収束するならば，数列

も収束する．数列(24)の要素は，数列

の部分和である．数列(25)の極限のよい推定値は，収束加速法を介してその数列の比較的少ない要素を使って計算することができることが多い．

"ExtrapolatingOscillatory"ストラテジーでは，(26)の積分に対してウィンの外挿法のNSumが使われる．(27)のそれぞれの積分は，振動法なしのNIntegrateで計算される．

"ExtrapolatingOscillatory"ストラテジーは，，，，，，，（ここで ，，， は実数定数）のいずれかの形式である(28)の振動カーネルにそのアルゴリズムを適用する．

例題の実装

以下の例題の実装は，"ExtrapolatingOscillatory"ストラテジーがどのように動作するかを示す．

次は区間で積分される振動関数の定義である．振動関数の零点は である：
区間の振動関数のプロットである：
次は2つの連続する零点の間で積分する関数の定義である．振動関数 の零点は である：
これは，数列の収束加速法（外挿）により計算される積分推定値である：
厳密な積分値である：
積分推定値は厳密値に非常に近い：
以下は"ExtrapolatingOscillatory"ストラテジーを使った，別の検証方法である：
"ExtrapolatingOscillatory"による積分推定値は，厳密値に非常に近い：

二重指数関数型振動積分

ストラテジー"DoubleExponentialOscillatory"は，，，（ は積分変数で ，， は定数）のいずれかの形式の被積分関数を持つ一次元無限領域上でゆっくりと減衰する振動積分のためのものである．

"DoubleExponentialOscillatory"を使った積分
オプション名
デフォルト値
MethodNone"DoubleExponentialOscillatory"が失敗したときに使用される積分ストラテジー
"TuningParameters"Automatic誤差推定の調整パラメータ
"SymbolicProcessing"Automatic記号的処理を実行する秒数

"DoubleExponentialOscillatory"のオプション

"DoubleExponentialOscillatory"はストラテジー"DoubleExponential"に基づくものであるが，"DoubleExponentialOscillatory"は積分区間の終点に二重指数関数的に達する変換を使用する代りに，およびの零点に二重指数関数的に達する変換を使用する．このアルゴリズムの理論的基礎および特性は[OouraMori91]，[OouraMori99]，[MoriOoura93]で説明されている．"DoubleExponentialOscillatory"の実装には，[OouraMori99]の公式および積分器設計が使われる．

"DoubleExponentialOscillatory"のアルゴリズムは，正弦積分

を使って説明する．次の変換

を考えてみる．ここで α および β は

を満足する定数である．α およびβ のパラメータは

を満足するよう選ばれる（[OouraMori99]より抜粋）．

変換(29)を(30)に適用し，

を得る．ω が正弦項でなくなっていることに注意されたい．等しいメッシュサイズ の台形公式を(31)に適用すると

が得られる．これは切り捨てられた級数の和

で近似される． および は

を満足するように選ばれる．被積分関数は(32)から分かるように，大きい負の において二重指数関数的に減衰する．「二重指数関数型ストラテジー」セクションの(33)である二重指数関数型変換も，大きい正の において被積分関数を二重指数関数的に減衰させるが，変換(34)は大きい正の で被積分関数を減衰させない．その代りにサンプル点が大きい正の においての零点に二重指数関数的に近付かせる．さらに

である．[OouraMori99]で説明されているように，はそのいずれの零点付近でも線形なので， がの零点に近付くにつれて被積分関数は二重指数関数的に減少する．これが(35)が二重指数関数型公式と考えられる理由である．

相対誤差は

を満足すると仮定されている．[OouraMori99]では， に提案された値はである．

公式は進行形にすることができないので，"DoubleExponentialOscillatory"は（[OouraMori99]で提唱されているように），異なる でからまでの積分推定を行う．所望の相対誤差が ならば，積分ステップは以下のようになる．

1. まず，

となるような を選び，で(36)を計算する．その結果を とする．

2. 次に と設定し，で(37)を計算する．その結果を とする．最初の積分ステップ の相対誤差は と仮定される．(38)より となるので，

（ここで は耐性係数であり，デフォルトは）を満足するならば，"DoubleExponentialOscillatory"は結果 で終了する．

3. もし(39)が成り立たないならば，

を計算し，で(40)を計算する．もし

が成り立てば，"DoubleExponentialOscillatory"は結果 で終了する．

4. もし(41)が成り立たないならば，

を計算し，で(42)を計算する．その結果を とする．もし

な成り立たないならば，"DoubleExponentialOscillatory"はメッセージNIntegrate::deonconを出力する．"DoubleExponentialOscillatory"メソッドオプションの値がNoneならば，が返される．そうでない場合は，"DoubleExponentialOscillatory"は"DoubleExponentialOscillatory"メソッドオプションで呼ばれたNIntegrateの結果を返す．

下の余弦積分

について，(43)に対応する変換は以下である．

一般化積分

次は正規化された発散積分 の記号計算である：
"DoubleExponentialOscillatory"は一般化された意味で，上の非正規化された積分を計算する：

発散フーリエ型積分に対する"DoubleExponentialOscillatory"の属性についての詳細は[MoriOoura93]に記載されている．

代数的でない被乗数

振動積分の記号的積分：
振動カーネルが代数的でない関数で乗算されても，"DoubleExponentialOscillatory"はよい結果を出す：
被積分関数とその振動カーネルのプロットである：

単純モンテカルロストラテジーと準モンテカルロストラテジー

単純モンテカルロ法は，積分領域に一様に分布した乱数点上で被積分関数値を平均することにより，指定された積分を推定する．点の数は，推定された標準偏差が指定された目標精度あるいは目標確度を満足するほど小さくなるまで増加される．モンテカルロ法で一様分布した乱数点ではなく，均等分布で確定的に生成された点の列が使われる場合，それは準モンテカルロ法と呼ばれる．

次は単純モンテカルロ積分である：
これは準モンテカルロ積分である：
オプション名
デフォルト値
Method"MonteCarloRule"モンテカルロ法の指定
MaxPoints50000サンプル点の最大数
"RandomSeed"Automatic乱数生成器をリセットする種
"Partitioning"1各軸に沿った積分領域の分割
"SymbolicProcessing"0記号的前処理を行う秒数

"MonteCarlo"オプション

オプション名
デフォルト値
MaxPoints50000サンプル点の最大数
"Partitioning"1各軸に沿った積分領域の分割
"SymbolicProcessing"0記号的前処理を行う秒数

"QuasiMonteCarlo"オプション

モンテカルロ法[KrUeb98]では， 次元積分 は次の期待（平均）値として解釈される．

ここで は， に対する一様分布，つまり確率密度vol(V)-1Boole(x∈V)の分布について，確率変数として解釈された関数 の平均値（期待値）である．領域 の特性関数はBoole(x∈V)で表され， の体積はで表される．

単純モンテカルロ法の積分値は積分則"MonteCarloRule"で生成される．積分値と誤差推定値の公式は「NIntegrateの積分則」の「MonteCarloRule」に示してある．

以下の積分

を考えてみる．もとの積分領域が互いに素な部分領域の集合， に分割されるならば，積分推定値は

であり，積分誤差は

となる．それぞれの部分領域で使用されるサンプル点の数は異なる場合があるが，モンテカルロ法では，すべての は等しい()．

分割 は層化と呼ばれ，各 は層と呼ばれる．層化は「単純モンテカルロ推定値の向上」のために使うことができる（「適応型モンテカルロ法」では再帰的層化が使われる）．

AccuracyGoalとPrecisionGoal

AccuracyGoalとPrecisionGoalのデフォルト値は，NIntegrateのモンテカルロ法が使われるときはそれぞれInfinityと2である．

MaxPoints

オプションMaxPointsは，積分のモンテカルロ指定値を計算するために使われる（擬似）乱数のサンプル点の最大数を指定する．

次はサンプル点の最大値に達し，NIntegrateがメッセージを出力して終了する例である：

"RandomSeed"

オプション"RandomSeed"の値は，積分点を生成するために使われる乱数生成器に種を蒔くために使われる．この点においては，モンテカルロ法で"RandomSeed"を使うことはSeedRandomおよびRandomRealを使うことに似ている．

"RandomSeed"を使うことにより，モンテカルロ積分の結果は再生することができる．次の2つの結果は同一である．

下は"RandomSeed"を使ったモンテカルロ積分である：
このモンテカルロ積分も同じ数値を返す：
次は，モンテカルロ積分で使われる最初の20の点である：
点はSeedRandomおよびRandomRealを使って作成された点と一致する：

層化抽出法の単純モンテカルロ積分

層化抽出法のモンテカルロ積分では，領域をいくつかの部分領域に分割し，それぞれの部分領域に別々に単純モンテカルロ推定法を適用する．

期待（平均）値公式である「単純モンテカルロストラテジーと準モンテカルロストラテジー」の最初の方程式(44)から，以下が求められる．

領域 が2つの半領域 と に二分されるものとする．は 上の の期待値，は 上の の分散とする．定理[PrFlTeuk92]より

が成り立つ．層化抽出法は単純モンテカルロのサンプリングの分散より大きいことの決してない分散を与える．

"MonteCarlo"ストラテジーに対して層を指定する方法が2つある．ひとつは変数範囲指定における「特異」点を指定するというもので，もうひとつはメソッドサブオプション"Partitioning"を使うというものである．

変数の範囲指定を使った，層化抽出法の単純モンテカルロ積分：
サブオプション"Partitioning"を使った，層化抽出法の単純モンテカルロ積分：

"Partitioning"に，整数変数の数に等しい長さ の整数のリストを与えると，積分領域の各次元 は 個の等しい部分に分割される．もし"Partitioning"に整数 を与えると，すべての次元が 個の等しい部分に分割される．

以下のグラフは"Partitioning"で指定された層化抽出法を示す．"MonteCarloRule"のオプション"Points"で指定されているように，それぞれのセルにつの点が含まれる：

層化抽出法の単純モンテカルロ積分は，積分変数の範囲が中間の特異点で与えられると指定することができる．

中間の特異点の指定を介した層化抽出法の単純モンテカルロ積分：

層化抽出法は，単純モンテカルロ積分推定の効率を向上させる．層の数が ならば，層化抽出法のモンテカルロ推定値の標準偏差は，単純モンテカルロ法による積分値の標準偏差の 分の1である（次の例題を参照）．

下のベンチマークは層化により収束が早まることを示している：

層化抽出法によるモンテカルロ積分の収束のスピードアップ

次の例題は，層の数が ならば，層化抽出法による積分値の標準偏差は，単純モンテカルロ法の積分値の標準偏差の 分の1であることを示している．

期待（平均）値公式(45)に基づく層化された積分定義である：
下の積分を考える：
上の積分は1から40までの層の数に対して1000個の点で近似される：
次は標準偏差と層化されていない単純モンテカルロ推定値との比である：
ratios〚i〛は層の数 i のモンテカルロ推定値に対する比である．これにより ratios に対する関数 の最小2乗フィットが試せる：
のフィットはに非常に近い係数を示す．これは 個の層が 倍速い収束を与えるという経験則の立証である．次は ratios と 最小2乗フィットのプロットである：

大域的適応型モンテカルロストラテジーと準モンテカルロストラテジー

大域的適応型モンテカルロストラテジーと準モンテカルロストラテジーは，最大分散推定値で部分領域を再帰的に半分に二分し，それぞれの半分について積分推定と分散推定を計算する．

適応型モンテカルロ積分の例である：
オプション名
デフォルト値
MethodMonteCarloRuleMonteCarloRule指定
"Partitioning"Automaticそれぞれの軸に沿った積分領域の初期分割
"BisectionDithering"0二分割軸に平行の領域側の真ん中からのオフセット
"MaxPoints"Automatic使用する（擬似）乱数サンプル点の最大数
"RandomSeed"Automatic（擬似）乱数サンプル点を生成するために使われる乱数の種

適応型（準）モンテカルロは，それぞれの部分領域で単純（準）モンテカルロ推定値を使用する．

部分領域二分のプロセスと後続する二重積分は大域的分散を減少させると期待され，これは再帰的層化抽出法と呼ばれる．これは，領域が互いに素な部分領域に分割されるならば，その領域上の確率変数の分散はそれぞれの部分領域上の確率変数の分散の和以上であるという定理に動機付けられている（「単純モンテカルロストラテジーと準モンテカルロストラテジー」の「層化抽出法の単純モンテカルロ積分」を参照のこと）．

大域的適応型モンテカルロストラテジー"AdaptiveMonteCarlo"は"GlobalAdaptive"に類似している．しかし以下のような重要な違いがある．

1.  "AdaptiveMonteCarlo"は特異点平坦化を使わないし，遅い収束およびノイズのある積分の検出器も持たない．

2.  "AdaptiveMonteCarlo"は二分次元をランダムに選ぶ．異なる座標の不規則な分離を避けるために，次元は，他の次元が二分に選ばれたときだけ繰り返される．

3.  "AdaptiveMonteCarlo"は真ん中から離れた部分領域を二分するよう調整することができる．詳細は"BisectionDithering"を参照のこと．

MinRecursionとMaxRecursion

適応型モンテカルロ法のオプションMinRecursionとMaxRecursionは"GlobalAdaptive"に対するのと同じ意味と機能を持つ．詳細は「MinRecursionとMaxRecursion」を参照のこと．

"Partitioning"

"AdaptiveMonteCarlo"のオプション"Partitioning"は積分の初期の層化を提供する．これは"MonteCarlo"ストラテジーの"Partitioning"と同じ意味と機能を持つ．

"BisectionDithering"

積分に，領域の真ん中に重要な部分を置く特別な対称性がある場合，二分を真ん中から少し離して行った方がよい．オプション"BisectionDithering"->dith の値は，分割次元側の分割分数がではなく におけるものであることを指定する．dith の符号は，ランダムに変化される．"BisectionDithering"に与えられるデフォルト値はである．dith に許される値は区間の中の実数である．

この関数を考える：
この積分を考える：
この積分は，二分でディザリングが使われない場合，つまり"BisectionDithering"に0が与えられる場合には，非常に過小評価される：
以下の画像は，なぜ積分が過小評価されるかを示している．黒い点が積分のサンプル点である．被積分関数のピークの半分が過少抽出されているのが分かる：
二分のディザリングをに指定すると，満足のいく推定値が与えられる：
下のプロットでは，被積分関数のピークがよりよく抽出されている：

二分割線の選択

多次元積分の場合，適応型モンテカルロアルゴリズムは2つの方法で積分領域の分割軸を選択する．1つは無作為抽出であり，もうひとつは各半分の積分推定値の分散を最小化することによる方法である．軸の選択は"MonteCarloRule"の責務となっている．

例題：単純モンテカルロとの比較

一般に，"AdaptiveMonteCarlo"ストラテジーは"MonteCarlo"のパフォーマンスに勝る．ここでは例題を使ってそれを示す．

次の関数を考える：
これは関数のプロットである：

以下のプロファイルから，"AdaptiveMonteCarlo"は単純"MonteCarlo"ストラテジーの約3分の1のサンプル点を使うことが分かる．

以下は"MonteCarlo"のサンプル点と所要時間である：
次は"AdaptiveMonteCarlo"のサンプル点と所要時間である：
これは厳密な結果である：
"MonteCarlo"を使った100回の積分にかかる時間である：
"MonteCarlo"積分は厳密な結果に引けを取らない．以下の数は，積分推定値の平均，積分推定値の相対誤差の平均，積分推定値の分散を示している：
"MonteCarlo"積分よりも数倍速い"AdaptiveMonteCarlo"を使った100回の積分にかかる時間である：
"AdaptiveMonteCarlo"積分の結果は厳密な結果に引けを取らない．以下の数は，積分推定値の平均の誤差，積分推定値の相対誤差の平均，積分推定値の分散を示している：

"MultiPeriodic"

"MultiPeriodic"ストラテジーはすべての積分を単位立方上の積分に変換し，その被積分関数をそれぞれの積分変数について1周期となるように期分けする．異なる変数には異なる期分け関数を適用するか，何も適用しない．"MultiPeriodic"は12以下の次元の積分に有効である．もし"MultiPeriodic"に高次元の積分が与えられると，"MonteCarlo"ストラテジーが使われる．

"MultiPeriodic"を使った積分の例である：
オプション名
デフォルト値
"Transformation"SidiSin被積分関数に適用される期分け変換
"MinPoints"0サンプル点の最少数
"MaxPoints"105サンプル点の最大数
"SymbolicProcessing"Automatic記号的前処理に使われる秒数

"MultiPeriodic"はストラテジー"Trapezoidal"の多次元一般化と見ることができる．これは準モンテカルロ法とも見ることができる．

"MultiPeriodic"では格子の積分則が使われる．[SloanJoe94]と[KrUeb98]を参照のこと．

ここで，における積分格子は，加算減算のもとで閉じられ， を含む の離散部分集合と理解される．格子積分則[SloanJoe94]は，以下の形式

の規則であり，ここではすべて に含まれる積分格子の点である．

"MultiPeriodic"が呼ばれると， 次元積分のオプション"Transformation"は，対応する変数を変換するために使われる1引数関数のリストを取る．もし"Transformation"に より小さい長さ のリストが与えられると，最後の関数 が最後の 積分変数に対して使われる．もし"Transformation"に関数が与えられると，すべての変数を変換するためにその関数が使われる．

が積分の次元であるとする．ならば，"MultiPeriodic"は期分け変換を適用した後で"Trapezoidal"を呼び出す．より大きい次元では，期分け変換を適用せずに"MonteCarlo"が呼ばれる．"MultiPeriodic"はに対していわゆる のコピールールを使用する．それぞれのに対して，"MultiPeriodic"は積分推定値のシーケンスを計算するために使われるコピールールの集合がある．これより少ない点の規則が先に使われる．規則の誤差推定値が目標精度を満足した場合，あるいはシーケンスの中の2つの異なる積分推定値が目標精度を満足した場合，積分は終了する．

異なる次元に対する規則の集合における のコピールールに対する点の数：

"MultidimensionalRule"との比較

一般に"MultiPeriodic"は"MultidimensionalRule"を使った"GlobalAdaptive"よりも遅い．低精度で高次元積分を計算するために，"MultiPeriodic"は結果をより速く出すことがある．

8つの引数の関数を定義する：
"MultidimensionalRule"の"MultiPeriodic"と"GlobalAdaptive"を使った の計算にかかる秒数：
"MultidimensionalRule"の"MultiPeriodic"と"GlobalAdaptive"を使った の計算に対する被積分関数の評価回数：

プリプロセッサ

すべてのストラテジーの機能は，積分の記号的前処理から拡張される．プリプロセッサは積分を他のストラテジー（プリプロセッサを含む）に委託するストラテジーとして見ることができる．

"SymbolicPiecewiseSubdivision"

"SymbolicPiecewiseSubdivision"は，区分的被積分関数を持つ積分を，それぞれの互いに素な積分領域において被積分関数が区分的でない積分に分割するプリプロセッサである．

オプション名
デフォルト値
MethodAutomatic積分が渡される積分ストラテジーあるいはプリプロセッサ
"ExpandSpecialPiecewise"Trueどの区分関数を拡張するか
TimeConstraint5区分的部分分割を試みる最大秒数
"MaxPiecewiseCases"100区分的プリプロセッサが返すことのできる部分領域の最大数
"SymbolicProcessing"Automatic記号的前処理を行う秒数

"SymbolicPiecewiseSubdivision"のオプション

このチュートリアルの最初で述べたように，NIntegrateはそれぞれ異なる被積分関数を持つ互いに素な領域を持つ積分を同時に実行することができる．したがって，"SymbolicPiecewiseSubdivision"を使った前処理の後，積分はNIntegrateに特異点指定のある領域が与えられたかのように続行される（これは同じ被積分関数を持つ互いに素な領域の積分を指定することと見ることができる）．例えば，"GlobalAdaptive"ストラテジーは二分による最大誤差を持つ領域の積分推定値を向上させようとし，どの被積分関数に対応するかにかかわらす，最大誤差領域を選ぶ．

以下は積分 の数値推定値に対するサンプル点である．プロット上では，被積分関数はord座標の順に x 座標でサンプリングされる．"GlobalAdaptive"は部分のサンプリングと部分のサンプリングを交互に行うとみることができる：
積分 Boole[x2+y2>1] sin(x2+y2)yx の数値推定値に対するサンプル点である．被積分関数は左に，サンプル点は右にプロットされる．積分は + + + に分割されており，そのためにサンプル点はに対して異なるパターンを形成するのである：
"ExpandSpecialPiecewise"

ある特定の区分関数上だけで区分的に展開した方がよい場合がある．このような場合は，オプション"ExpandSpecialPiecewise"にその区分的展開を実行する関数のリストを与えることができる．

下のモンテカルロ積分はBoole上に限ると区分的展開の方が速い
次はBooleとAbsの両方における区分的展開を行うモンテカルロ積分である：

"EvenOddSubdivision"

"EvenOddSubdivision"は，領域が原点を中心に対称であり，被積分関数が偶関数または奇関数となっている場合に，積分領域を減少させるプリプロセッサである．奇関数の積分の収束はデフォルトで検証される．

オプション名
デフォルト値
MethodAutomatic積分が渡される積分ストラテジーあるいはプリプロセッサ
VerifyConvergenceAutomatic奇関数の積分が検出されたときに，収束を検証する
"SymbolicProcessing"Automatic記号的前処理を実行する秒数

"EvenOddSubdivision"のオプション

被積分関数が偶関数であり，積分領域が原点を中心として対称な場合，積分は積分領域の一部だけで積分し，対応する因子で乗算することにより計算することができる．

以下は偶関数および前処理のないサンプル点のプロットである：
次は"EvenOddSubdivision"が適用された後にNIntegrateで使われるサンプル点である．サンプル点は領域にあることに注意する：
変換定理

プリプロセッサ"EvenOddSubdivision"は次の定理に基づいている．

定理： 次元積分

を仮定した場合，ある に対して，下の等式が成り立つとする．

a)

b) すべての について

換言すると， の範囲は原点を中心として対称であり，変数 の境界は についての偶関数である．

それならば

a) 積分は

に等しい．これは被積分関数が について偶関数，つまり以下の場合である．

b) 積分は，被積分関数が について奇関数の場合，つまり下の場合にに等しい．

上の定理は積分上で何回か適用することができる．

定理を例示するために，積分 を考えてみる．これは に対して対称であり， の被積分関数と境界は に関して偶関数である．

次は"EvenOddSubdivision"を適用しないサンプル点（黒）および"EvenOddSubdivision"を適用したサンプル点（赤）のプロットである：

の境界が に関して偶関数でないならば， に対する対称性は壊れる．例えば，積分 にはNIntegrateが使える対称性はない．

次は"EvenOddSubdivision"を適用したサンプル点（赤）のプロットである．この領域には についての対称性はない：
"VerifyConvergence"
次の発散積分 を考える．NIntegrateはそれが対称領域上の奇関数であると検出し， を積分しようと試みる（つまり の収束をチェックする）．ncvbメッセージにより示されるように，収束には達さなかったので，NIntegrateは積分が発散するかもしれないというメッセージoidivを出力する：
オプションVerifyConvergenceがFalseに設定されると，積分が奇関数であると分かった後，収束の検証（および被積分関数の評価）は行われない：

"OscillatorySelection"

"OscillatorySelection"は一次元振動積分の効率的な評価のために特化されたアルゴリズムを選ぶプリプロセッサである．

それぞれの積分範囲上で"OscillatorySelection"は，被積分関数がフーリエの有限範囲型，フーリエの無限範囲型（"DoubleExponentialOscillatory"を参照），ベッセルの無限範囲型（"ExtrapolatingOscillatory"を参照），レビン型（"LevinRule"を参照）のいずれか，ある９いはどの特殊な振動型でもないかを検出する．

オプション名
デフォルト名
"BesselInfiniteRangeMethod"Automatic無限範囲のベッセル積分に対する方法
"FourierFiniteRangeMethod"Automatic有限範囲のフーリエ積分に対する方法
"FourierInfiniteRangeMethod"Automatic無限範囲のフーリエ積分に対する方法
"LevinMethod"Automaticレビン型の振動積分に対する方法
Method"GlobalAdaptive"非振動積分に対する方法
"TermwiseOscillatory"False総和の中の項を別々に処理するかどうか
"SymbolicProcessing"5記号処理を行う秒数

"OscillatorySelection"のオプション

NIntegrateではデフォルトで"OscillatorySelection"プリプロセッサが使われる：
"OscillatorySelection"プリプロセッサがないと，NIntegrateはそのデフォルトのオプション設定では収束に達しない：

プリプロセッサ"OscillatorySelection"は"SymbolicPiecewiseSubdivision"プリプロセッサの内的出力と動作するよう設計されている．"OscillatorySelection"自体は原点を含む，または拡張・変換が必要な振動カーネルを持つ振動積分を，振動アルゴリズムが設計された形式に分割する．

次の区分関数の積分では，一次元積分に対する特化された積分ストラテジーすべてが"OscillatorySelection"により自動的に選ばれる．この積分では，プリプロセッサ"SymbolicPiecewiseSubdivision"が積分を4つの異なる積分に分割する．これらの積分のそれぞれについて，"OscillatorySelection"は適切な特化されたアルゴリズムを選ぶ：
次の表は，上の積分における各部分積分のアルゴリズムを指定するために使われる"OscillatorySelection"オプションの名前を示している：
x∈(-∞,0]"BesselInfiniteRangeMethod"
x∈[0,20]"FourierFiniteRangeMethod"
x∈[30,∞)"FourierInfiniteRangeMethod"
x∈[20,30]Method
この例では，"DoubleExponentialOscillatory"が2度呼ばれている．"DoubleExponentialOscillatory"はフーリエ積分に対する特殊アルゴリズムであり，公式 により，被積分関数は2つのフーリエ被積分関数の総和になる：
"OscillatorySelection"が公式 を使ったことを示すために，上の積分を「手動」で分割する．結果はすぐ上の結果と同一である：

オプション"FourierFiniteRangeMethod"に対する値Automaticは，オプションMethodにより指定される積分ストラテジーが"GlobalAdaptive"か"LocalAdaptive"のいずれかであれば，そのストラテジーが有限領域のフーリエ積分に使われ，そうでなければ"GlobalAdaptive"が使われることを意味している．

非振動積分については"DoubleExponential"ストラテジーを使い，有限領域振動積分については"LocalAdaptive"を使う区分的関数積分である：
これらは前の積分のサンプル点であるが，デフォルト設定を使ったものである．左側の画像のの間のパターンは，局所的適応型積分法では典型的である．つまり，3つの部分への再帰的分割が見られる（オプション"Partitioning"->3が"LocalAdaptive"に与えられたためである）．右の画像のを超えた部分のパターンは"GlobalAdaptive"から来ている．最初の画像のの間のパターンは，二重指数関数的積分公式では典型的である．同じパターンが2つ目の画像のの間で見られる．これは"GlobalAdaptive"がデフォルトで"DoubleExponential"特異点ハンドラを使うためである：

特定の振動メソッドの適用が特定のタイプの振動積分に要求されている場合，"OscillatorySelection"の対応するオプションを変更するか，NIntegrateのMethodオプションをプリプロセッサの"OscillatorySelection"なしで使うかしなければならない．

これは無限領域振動積分のすべてに対して"ExtrapolatingOscillatory"を使用する，区分関数積分である：
"ExtrapolatingOscillatory"がメソッドとして与えられると，"OscillatorySelection"はそれを無限領域振動積分に使用する：
上の積分はNIntegrateのデフォルトオプションを使った方が速い．デフォルトで適用される次の積分"OscillatorySelection"では"DoubleExponentialOscillatory"が使われる：

"UnitCubeRescaling"

"UnitCubeRescaling"は，積分領域を単位立方あるいは超立方に変換するプリプロセッサである．もとの被積分関数の変数が置き換えられると，結果は変換のヤコビアンで乗算される．

オプション名
デフォルト値
"FunctionalRangesOnly"Trueどの領域を単位立方に変換するか
Method"GlobalAdaptive"積分が渡される積分ストラテジーあるいはプリプロセッサ
"SymbolicProcessing"Automatic記号的処理を行う秒数

"UnitCubeRescaling"のオプション

次では，単位立方の再スケールが使われ，その後の計算よりも速い：
この積分は単位立方の再スケールを使わない．これは前の計算よりも約3倍遅い：

"UnitCubeRescaling"は下の積分

を超立方上の積分に変換する．と が有限で が区分的連続関数であるとすると，"UnitCubeRescaling"により使われる変換は

である．この変換のヤコビアンは

である． 番目の軸に対して， と のうちの一方もしくは両方が無限ならば，(46)の に対する公式はをにマップする非アフィン変換である．NIntegrateは次の変換を使用する．

ここで である．

積分領域の境界が定数（有限・無限）ならば，"UnitCubeRescaling"を適用することで，被積分関数はより複雑になる．NIntegrateには効率的なアフィンと無限内部変数変換があるため，積分プロセスは遅くなる．積分領域境界のいくつかが関数ならば，"UnitCubeRescaling"を適用することで積分は速くなる．それは，積分変数を含む計算が被積分関数が評価されたときしか実行されないからである．このようなパフォーマンスについての考えがあるため，"UnitCubeRescaling"にはオプション"FunctionalRangesOnly"があるのである．"FunctionalRangesOnly"がTrueに設定されると，再スケールは多次元関数範囲にだけ適用される．

以下の積分は単位立方の再スケールを使用する：
この積分は単位立方の再スケールを使わない．これは前の計算よりもほぼ2倍速く実行される：
例題の実装

"UnitCubeRescaling"で使用される変換プロセスは関数FRangesToCubeで実装される以下のものと同じである（「Duffyの座標の一般化と例題実装」でも定義してある）．

この関数は，積分領域のリストおよび直方体の面のリストまたは超立方の面のリストに対する変換(47)およびそのヤコビアン(48)を提供する：

変換(49)のそれぞれの変換はRescaleで実行することができる．

指定の軸 について，軸に対してすでに導出されている変換規則は， 番目の軸に沿った境界線を再スケールする前にもとの境界線に適用する必要がある．

に対する変換規則とヤコビアンである：
変換の関数への適用：
に対する変換規則とヤコビアン：
に対する変換規則とヤコビアン：

"SymbolicPreprocessing"

"SymbolicPreprocessing"は他のプリプロセッサのオンとオフを簡約するために作られた合成プリプロセッサである．

オプション名
デフォルト値
MethodAutomatic積分が渡される積分ストラテジーあるいはプリプロセッサ
"SymbolicPiecewiseSubdivision"True区分的部分分割
"EvenOddSubdivision"True偶・奇部分分割
"OscillatorySelection"True振動関数での積の検出
"UnitCubeRescaling"Automatic単位超立方の再スケール
"SymbolicProcessing"Automatic記号処理を行う秒数

"SymbolicPreprocessing"オプション

"UnitCubeRescaling"がAutomaticに設定されると，それは多次元関数範囲にのみ適用される．

次は異なるプリプロセッサを組み合せて適用した yx の積分の例である：

例題と応用

閉曲線積分

次の関数は極座標のパラメータ化で与えられる閉曲線の体積を計算する：
次はIntegrateを使った半径2および3の楕円の円周である：
次は，同じ関数を使った半径2および3の楕円の円周近似である：
この近似は厳密値に引けを取らない：

フーリエ級数の計算

以下は関数の切断されたフーリエ級数近似を計算するWolfram言語関数である：
Integrateを使った上の のフーリエ近似である：
これは とフーリエ級数近似のプロットである：
これはNIntegrateを使った上のSin[x3+]の60項フーリエ近似である．Integrateが使われると，計算は非常に遅い：
これはSin[x3+]とフーリエ級数近似のプロットである：