不確実性のある回帰

混合密度ネットワーク
このセクションでは，混合密度ネットワークを用いて，回帰問題における不確実性をモデル化する方法を示す．このようなネットワークは，入力として x 値を取り，出力として 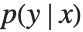を近似する混合分布のパラメータを生成することで，事後分布 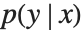をモデル化する．
次のコードは対応する x 値および y 値の形で合成訓練データを生成する．このデータには各 x 値に対していくつかの y 値が存在することがあるため，通常の関数 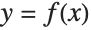を表さない．また，このデータには多量のノイズが含まれている：
通常の回帰ネットワークは，入力値 x（x と y はスカラー，ベクトル，行列等）が与えられると，1つの y を予測する．密度ネットワークの基本的な考え方は，y 値の分布を計算することである．ネットワークは，この分布のパラメータを x の関数として学習する．「混合」密度ネットワークは単一分布を混合したものを学習する．次の例では6つのガウス関数の混合分布を使う．
入力数値を1つ取り，多層パーセプトロンを使って3つの別々のベクトルを生成するネットを構築する． それぞれのベクトルには6つの別々のガウス関数の成分の対するパラメータを表す6つの数が含まれている．このベクトルのうちの2つ，'mean'と'stddev'はガウス関数の平均と標準偏差を表す．最後のベクトル'weight'は，これらの6つのガウス関数を「混合」して1つの分布を生成する方法を表す確率ベクトルである．Expアクティベーションを使って標準偏差が必ず正になるようにし，SoftmaxLayerを使って重みの和が必ず1になるようにする：
次に，このパラメータネットを訓練する，より大きいネットワークを構築する．大きいネットワークは，データ分布から実際の x 値と y 値を取り，負の対数尤度を計算する．負の対数尤度は，パラメータネットが表すモデルの下にデータがある可能性を測定するものである．負の対数尤度を最小限にすることによって，実際のデータの尤度を最大限にすることになる．これは確率モデルを訓練する一般的な方法である．
訓練ネットは，パラメータネットにより生成された6つのガウス関数の下の1つの y 値の尤度を計算する．これら別々の尤度を混合ガウス関数の単独の尤度にまとめるために，重みベクトルを使って重み付き総和を実行する．最後に負の対数を取る．
ガウス尤度を計算するThreadingLayer，6つのガウス関数全体の尤度の重み付き総和を取るDotLayer，これを負の対数尤度に変換するElementwiseLayerを使って，訓練ネットワークを構築する：
うまくいっているかを確認するために，1つのデータ点上でランダムに初期化されたネットの損失を見てみる．
NetInitializeを使ってネットをランダムに初期化し，それを1つの入力に適用する：
これでモデルが訓練できるようになった．これはデータ集合のすべての点を生成するモデルの尤度を同時に最大化することに相当する．訓練の後，訓練されたネットの内部からパラメータネットを抽出する．訓練データに対する負の対数尤度を計算する必要はもうないので，訓練ネットは必要ない．パラメータネットは，x 値が与えられると平均，標準偏差，重みの連想を生成する．
NetTrainを使って3000ラウンドでネットを訓練する．LossFunction"Loss"と指定して， NetTrainが自動的に損失層を加えようとするのではなく，「Loss」というポートから出力を直接最小化するようにする：
NetExtractを使って，訓練された最終的なネットから訓練されたパラメータネットを抽出する：
訓練されたパラメータネットを入力に適用する：
x 値が与えられたときにMixtureDistributionを構築する関数を定義する：
特定の x 値で関数を適用する：
分布から新しい y 値を抽出する：
この分布の確率密度関数をプロットする．これは事後分布 である：
下のデータの中の各 x 値について，モデルによって計算された事後分布 から1つのサンプルを取る：
下のデータのプロットとモデルからのサンプルを重ねてみる：
「密度モデル」は特定の値 x と y に対する確率密度 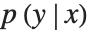を計算する効率がよいため，これを学習した．尤度を計算するネットを作成するために，訓練されたネットから負の対数尤度を計算する層を削除することができる．
NetDeleteを使って，負の対数尤度を計算するElementwiseLayerを削除する：
この密度モデルの動作を可視化する方法はいろいろある．一番簡単なのは，x 値と y 値の密な格子において尤度を抽出して，密度プロットを生成するというものである．また，各成分を可視化して，その平均と重みの値がどのように変化するかを，x の関数として可視化することもできる．
CoordinateBoundsArrayを使って{x,y}ペアの格子を作成し，x 値と y 値の別々のリストに平滑化する：
尤度ネットを使って，これらの値に対する確率を1回で効率的に評価し，再び行列を形成するために確率を非平滑化する：
行列をプロットする：
x 値の範囲上で混合パラメータを評価する：
変数「means」と「stddevs」に，それぞれの x の位置に対する6つのガウス関数の成分のパラメータが含まれるようになった．「weights」には混合の重みが含まれる：
個々の混合成分をエンベロープとしてプロットする．ここで実線は各成分の平均であり，陰影付きの領域は標準偏差の対象となる y 値の範囲を示す．
直線 mean-stddev，mean，mean+stddev，およびそれらの間に適切な陰影をプロットすることによって単独の成分をプロットする関数を定義する．その後このこれらのプロットを単独のプロットに合成する：
上から分かるように，与えられた成分に関連付けられた標準偏差が，対応する混合の重みがゼロに近付くときに非常に大きくなることは珍しくない．これは，その成分がモデルおよび損失に寄与していないからである．
次に混合の重みを x 値の関数としてプロットする．ここで色は上のグラフで示されている成分と一致する．
StackedListPlotを使って，互いに重なり合った6つの重みの値を x 値の関数としてプロットする．パラメータネット内にSoftmaxLayer[]があるため，それぞれの x 値において，総和は1になる：
最後に，混合成分の平均とその混合の重みを同時に可視化する．成分に関連付けられた直線を，その混合の重みが減少するにつれて，次第に消えていくようにする．これをもとのデータ集合と比較すると，各 x 値における主要な混合成分が，その x 値におけるもとのデータ集合の y 値のクラスタ化をいかに反映しているかが簡単に分かる．
ColorFunctionオプションを使って， それぞれのListLinePlotが対応する平均の直線を消すようにする．重みのリストに基づく補間関数で消去の程度を調べる：