represents a net layer that applies a unary function f to every element of the input array.
ElementwiseLayer["name"]
applies the function specified by "name".


ElementwiseLayer
represents a net layer that applies a unary function f to every element of the input array.
ElementwiseLayer["name"]
applies the function specified by "name".
Details and Options



- The function f can be any one of the following: Ramp, LogisticSigmoid, Tan, Tanh, ArcTan, ArcTanh, Sin, Sinh, ArcSin, ArcSinh, Cos, Cosh, ArcCos, ArcCosh, Cot, Coth, ArcCot, ArcCoth, Csc, Csch, ArcCsc, ArcCsch, Sec, Sech, ArcSec, ArcSech, Haversine, InverseHaversine, Gudermannian, InverseGudermannian, Log, Exp, Sqrt, CubeRoot, Abs, Gamma, LogGamma, Erf, InverseErf, Erfc, InverseErfc, Round, Floor, Ceiling, Sign, FractionalPart, IntegerPart, Unitize, KroneckerDelta.
- In general, f can be any object that when applied to a single argument gives any combination of Ramp, LogisticSigmoid, etc., together with numbers, Plus, Subtract, Times, Divide, Power, Surd, Min, Max, Clip, Mod, Threshold, Chop and some logical operations using If, And, Or, Which, Piecewise, Equal, Greater, GreaterEqual, Less, LessEqual, Unequal, Negative, NonNegative, Positive, NonPositive, PossibleZeroQ.
- ElementwiseLayer supports the following values for "name":
-
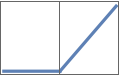
"RectifiedLinearUnit" or "ReLU" Ramp[x] 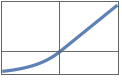
"ExponentialLinearUnit" or "ELU" x when x≥0 Exp[x]-1 when x<0 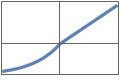
"ScaledExponentialLinearUnit" or "SELU" 1.0507 x when x >= 0 1.758099340847161` (Exp[x]-1) when x<0 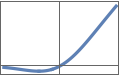
"GaussianErrorLinearUnit" or "GELU" 0.5 x(1+Erf[x/Sqrt[2]]) 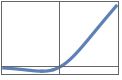
"Swish" x LogisticSigmoid[x] 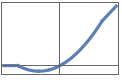
"HardSwish" x Min[Max[x+3,0],6]/6 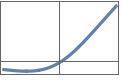
"Mish" x Tanh[Log[1+Exp[x]]] 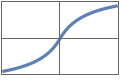
"SoftSign" x/(1+Abs[x]) 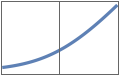
"SoftPlus" Log[Exp[x]+1] 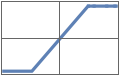
"HardTanh" Clip[x,{-1,1}] 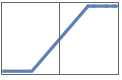
"HardSigmoid" Clip[(x+1)/2, {0,1}] 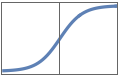
"Sigmoid" LogisticSigmoid[x] - ElementwiseLayer[…][input] explicitly computes the output from applying the layer.
- ElementwiseLayer[…][{input1,input2,…}] explicitly computes outputs for each of the inputi.
- When given a NumericArray as input, the output will be a NumericArray.
- ElementwiseLayer is typically used inside NetChain, NetGraph, etc.
- ElementwiseLayer exposes the following ports for use in NetGraph etc.:
-
"Input" an array of arbitrary rank "Output" an array with the same dimensions as the input - When it cannot be inferred from other layers in a larger net, the option "Input"->{n1,n2,…} can be used to fix the input dimensions of ElementwiseLayer.
- Options[ElementwiseLayer] gives the list of default options to construct the layer. Options[ElementwiseLayer[…]] gives the list of default options to evaluate the layer on some data.
- Information[ElementwiseLayer[…]] gives a report about the layer.
- Information[ElementwiseLayer[…],prop] gives the value of the property prop of ElementwiseLayer[…]. Possible properties are the same as for NetGraph.
Examples
open all close allBasic Examples (2)
Create an ElementwiseLayer that computes Tanh of each input element:
Create an ElementwiseLayer that multiplies its input by a fixed constant:
Scope (3)
Create a ElementwiseLayer that computes a "hard sigmoid":
Apply the layer to a batch of inputs:
Plot the behavior of the layer:
Create an ElementwiseLayer that takes vectors of size 3:
Apply the layer to a single vector:
When applied, the layer will automatically thread over a batch of vectors:
Create an ElementwiseLayer that computes a Gaussian:
Applications (3)
Train a 16-layer-deep, self-normalizing network described in "Self-Normalizing Neural Networks", G. Klambauer et. al., 2017, on the UCI Letter dataset. Obtain the data:
Self-normalizing nets assume that the input data has mean of 0 and variance of 1. Standardize the test and training data:
Verify that the sample mean and variance of the training data are 0 and 1, respectively:
Define a 16-layer, self-normalizing net with "AlphaDropout":
Compare the accuracy against the "RandomForest" method in Classify:
Allow a classification network to deal with a "non-separable" problem. Create a synthetic training set consisting of points on a disk, separated into two classes by the circle r=0.5:
Create a layer composed of two LinearLayer layers, and a final transformation into a probability using an ElementwiseLayer:
Train the network on the data:
The net was not able to separate the two classes:
Because LinearLayer is an affine layer, stacking the two layers without an intervening nonlinearity is equivalent to using a single layer. A single line in the plane cannot separate the two classes, which is the level set of a single LinearLayer.
Train a similar net that has a Tanh nonlinearity between the two layers:
The net can now separate the classes:
Binary classification tasks require that the output of a net be a probability. ElementwiseLayer[LogisticSigmoid] can be used to take an arbitrary scalar and produce a value between 0 and 1. Create a net that takes a vector of length 2 and produces a binary prediction:
Train the net to decide if the first number in the vector is greater than the second:
Evaluate the net on several inputs:
The underlying output is a probability, which can be seen by disabling the "Boolean" decoder:
Properties & Relations (1)
ElementwiseLayer is automatically used when an appropriate function is specified in a NetChain or NetGraph:
Possible Issues (3)
ElementwiseLayer cannot accept symbolic inputs:
Certain choices of f can produce failures for inputs outside their domain:
Certain functions are not supported directly:
Approximate the Zeta function using a rational function:
The approximation is good over the range (-10,10):
Construct an ElementwiseLayer using the approximation:
Measure the error of the approximation on specific inputs:
The network will fail when evaluated at a pole:
Tech Notes
Related Guides
History
Introduced in 2016 (11.0) | Updated in 2017 (11.1) ▪ 2017 (11.2) ▪ 2018 (11.3) ▪ 2021 (12.3) ▪ 2021 (13.0) ▪ 2022 (13.1)
Text
Wolfram Research (2016), ElementwiseLayer, Wolfram Language function, https://reference.wolfram.com/language/ref/ElementwiseLayer.html (updated 2022).
CMS
Wolfram Language. 2016. "ElementwiseLayer." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/ElementwiseLayer.html.
APA
Wolfram Language. (2016). ElementwiseLayer. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ElementwiseLayer.html
BibTeX
@misc{reference.wolfram_2025_elementwiselayer, author="Wolfram Research", title="{ElementwiseLayer}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/ElementwiseLayer.html}", note=[Accessed: 22-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_elementwiselayer, organization={Wolfram Research}, title={ElementwiseLayer}, year={2022}, url={https://reference.wolfram.com/language/ref/ElementwiseLayer.html}, note=[Accessed: 22-January-2026]}