NetGraph

NetGraph[{layer1,layer2,…},{m1n1,m2n2,…}]

specifies a neural net defined by a graph in which the output of layer mi is given as input to layer ni.

NetGraph["name1"layer1,"name2"layer2,…,{"namem1""namen1",…}]

specifies a net with explicitly named layers.

NetGraph[layer]

converts a layer or a NetChain into an equivalent minimal NetGraph.

Details and Options

  • NetGraph is typically used to combine neural networks operations with multiple inputs or outputs for operations like residual connections, concatenation, attention and more. The result is a directed acyclic graph.
  • Input or output ports for the entire NetGraph can be created by specifying NetPort["input"]… or …NetPort["output"] in the list of connections.
  • A linear chain of connections within the graph can be specified as layer1layer2…layern, which will cause each layeri to be connected to layeri+1.
  • If the n^(th) layer, or a layer named "layer", has more than one input port or more than one output port, these can be disambiguated by writing NetPort[n,"port"] or NetPort["layer","port"].
  • If a layer has a port that accepts multiple inputs, such as CatenateLayer or ThreadingLayer, multiple connections can be made simultaneously by writing {m1,m2,…}n, which is equivalent to …,m1n,…,m2n,…. The inputs mi are always passed to n in the order m1,m2,….
  • If one or more input or output ports of any layers are left unconnected, these will become ports of the entire NetGraph.
  • If multiple output ports of layers are left unconnected and share the same name "Output", they will become separate ports of the entire NetGraph with names "Output1", "Output2", etc.
  • Some output ports can be left muted by writing NetPort[layer,"port"]None.
  • Specifying the array shapes, a NetEncoder or a NetDecoder for a port can be done with options of the form "port"shape, where shape can be:
  • "Real"a single real number
    "Integer"a single integer
    Restricted["Integer",n]an integer between 1 and n
    Restricted["Integer",{m,n}]an integer between m and n
    na vector of length n
    {n1,n2,…}an array of dimensions n1×n2×…
    "Varying"a vector whose length is variable
    {"Varying",n2,n3,…}an array whose first dimension is variable and remaining dimensions are n2×n3×…
    NetEncoder[…]an encoder (for input ports)
    NetEncoder[{…,"Dimensions"{n1,…}}]an encoder mapped over an array of dimensions n1×…
    NetDecoder[…]a decoder (for output ports)
    NetDecoder[{…,"InputDepth"n}}]a decoder applied to an array of rank n
    FeatureExtractorFunction[…]a feature extractor function
  • NetGraph supports the following special layer specifications in the list of the first argument:
  • Ramp,LogisticSigmoid,…ElementwiseLayer[f]
    Plus,Times,Divide,…ThreadingLayer[f]
    nLinearLayer[n]
    {layer1,layer2,…}NetChain[{layer1,layer2,…}]
  • The following training parameter can be included:
  • LearningRateMultipliersAutomaticlearning rate multipliers for trainable arrays in the net
  • For a net with a single input port, NetGraph[…][data] gives the result of applying the net to data.
  • For a net with multiple input ports, NetGraph[…][<|port1data1,…|>] provides data to each port.
  • For a net with a single output port, NetGraph[…][data] gives the output for that port. If a NetDecoder with a property prop is attached to the output, NetGraph[…][data,prop] computes that property.
  • NetGraph[…][data,"Properties"] can be used to get the list of possible properties.
  • For a net with multiple output ports, NetGraph[…][data] gives an association of the outputs for all ports. NetGraph[…][data,NetPort["oport"]] gives the output for the output port named "oport".
    If a NetDecoder with a property prop is attached to this output, NetGraph[…][data,NetPort["oport"]prop] computes the property for that port.
  • NetGraph[…][data,NetPort["oport"]"Properties"] can be used to get the list of possible properties for a given port.
  • NetGraph[…][data,NetPortGradient["port"]] gives the gradient of the output with respect to the value of the input port "port".
  • NetGraph[…][data,NetPortGradient[{layer1,…,"array"}]] gives the gradient of the output with respect to an array of a nested layer.
  • NetGraph[…][data,NetPortGradient[All]] yields an association with all the gradients.
  • NetGraph[…][data,{spec1,spec2,…}] gives an association of the outputs for all specifications. Each specification speci can be a NetPort setting, a reference to a NetDecoder property or a NetPortGradient.
  • NetGraph[…][data,…,opts] specifies that options should be used in applying the net to data. Possible options include:
  • BatchSizeAutomaticfor lists of inputs, the number of inputs to evaluate at once
    NetEvaluationMode"Test"what mode to use in performing evaluation
    RandomSeedingAutomatichow to seed pseudorandom generators, if any
    TargetDevice"CPU"the target device on which to perform evaluation
    WorkingPrecision"Real32"the numerical precision used for evaluating the net
  • Possible settings for WorkingPrecision include:
  • "Real32"use single-precision real (32-bit)
    "Real64"use double-precision real (64-bit)
    "Mixed"use half-precision real for certain operations
  • WorkingPrecision"Mixed" is only supported for TargetDevice"GPU", where it can result in significant performance increases on certain devices.
  • When given a NumericArray as input, the output will be a NumericArray. In this case, its numeric type is derived from WorkingPrecision.
  • With the setting NetEvaluationMode"Training", layers such as DropoutLayer will behave as they do for training rather than ordinary evaluation.
  • The StandardForm of NetGraph shows the connectivity of layers in the graph and annotates edges with the dimensions of the array that the edge represents. Clicking a layer or a port in the graph shows more information about that layer or port.
  • Normal[NetGraph[…]] returns a list or association of the layers used to construct the graph. EdgeList[NetGraph[…]] returns the list of connections in the graph.
  • NetGraph[…][[spec]] extracts the layer specified by spec from the net.
  • Transformation on NetGraph[…] network can be achieved with NetReplacePart, NetReplace, NetRename, NetFlatten, NetDelete, NetTake, …
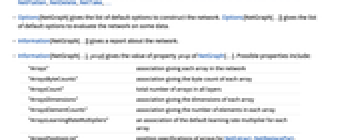
  • Options[NetGraph] gives the list of default options to construct the network. Options[NetGraph[…]] gives the list of default options to evaluate the network on some data.
  • Information[NetGraph[…]] gives a report about the network.
  • Information[NetGraph[…],prop] gives the value of property prop of NetGraph[…]. Possible properties include:
  • "Arrays"association giving each array in the network
    "ArraysByteCounts"association giving the byte count of each array
    "ArraysCount"total number of arrays in all layers
    "ArraysDimensions"association giving the dimensions of each array
    "ArraysElementCounts"association giving the number of elements in each array
    "ArraysLearningRateMultipliers"an association of the default learning rate multiplier for each array
    "ArraysPositionList"position specifications of arrays for NetExtract, NetReplacePart, LearningRateMultipliers, …
    "ArraysSizes"association giving the size of each array
    "ArraysTotalByteCount"total number of bytes in all arrays in all layers
    "ArraysTotalElementCount"total number of elements in all arrays
    "ArraysTotalSize"total size of all arrays in all layers
    "FullSummaryGraphic"graphic representing connectivity of all layers in the net, at any depth
    "InputForm"expression to reconstruct the net
    "InputPortNames"list of names of input ports
    "InputPorts"association of input port shapes
    "Layers"association giving each layer in the network
    "LayersCount"total number of layers
    "LayersGraph"graph representing layer connectivity
    "LayersList"list of all layers
    "LayerTypeCounts"how many times each type of layer occurs in the network
    "MXNetNodeGraph"raw graph of underlying "MXNet" operations
    "MXNetNodeGraphPlot"annotated graph of "MXNet" operations
    "OutputPortNames"list of names of output ports
    "OutputPorts"association of output port shapes
    "Properties"available properties
    "RecurrentStatesCount"number of recurrent states in the net
    "RecurrentStatesPositionList"position specifications of recurrent states for NetStateObject
    "SharedArraysCount"total number of shared arrays
    "SummaryGraphic"graphic representing connectivity of layers
  • The properties "ArrayByteCount" and "ArraysTotalByteCount" treat all arrays as if they have already been initialized.

Examples

open allclose all

Basic Examples  (3)

Create a residual net:

Initialize all arrays in the net:

Apply the net to an input:

Convert a NetChain into a NetGraph:

Nest a layer into a NetGraph:

Scope  (14)

Construction  (6)

Construct a net consisting of a linear chain:

Some layer names can be omitted and consecutive edge rules can be chained:

The final expressions are identical:

Construct a net graph with an operation requiring two inputs:

Construct a net graph with multiple inputs:

Construct a net graph with multiple outputs:

Construct a net graph with explicitly named layers:

Construct a net graph from existing NetGraph or NetChain:

Special Construction with NetPort  (3)

Create a net where the output is the final internal state of a LongShortTermMemoryLayer:

Apply the net to an input:

Modify the connectivity of an existing graph:

Connect to the inner port of a wrapped NetChain:

Flatten the resulting NetGraph:

Evaluation  (3)

Construct a NetGraph:

Apply the net to an input:

Apply the net to a NumericArray:

Apply the net using double-precision real:

Apply the net using the system's default GPU (if any):

Compute the first-order derivatives of the net:

Create a net with a class decoder:

Evaluate the net:

Retrieve a property of the decoder by specifying a second argument:

Construct a net that explicitly computes a loss:

Initialize the net and evaluate it on an input:

Properties  (2)

Construct a net:

Extract a given layer by position:

Get the list of layers:

Construct a net with explicitly named layers:

Extract a given layer by name:

Get all of the arrays in the net:

Get all layers in an association:

Get the list of edges:

Applications  (1)

Perform multitask learning by creating a net that produces two separate classifications. First, obtain training data:

The training data consists of an image and the corresponding high-level and low-level labels:

Extract the unique labels from the "Label" and "SubLabel" columns:

Create a base convolutional net that will produce a vector of 500 features:

Create a NetGraph that will produce separate classifications for the high-level and low-level labels:

Train the network:

Evaluate the trained network on some example images:

Get probabilities for a single image:

From a random sample, select the images for which the net produces highest and lowest entropy predictions for "Label":

Use NetTake to produce a sub-network that computes only "SubLabel" predictions:

Make a prediction on a single image:

Properties & Relations  (4)

NetChain objects can be used as layers in a NetGraph:

NetGraph objects with one input and one output can be used as layers inside NetChain objects:

The layers used to construct a NetGraph can be extracted using Normal:

Use Information[graph,"SummaryGraphic"] to get a Graphics[…] expression that shows the underlying connectivity of a graph:

Possible Issues  (1)

The order in which edges are defined in a NetGraph can matter. Create a NetGraph that computes a matrix-vector dot product:

Reversing the order in which the edges are defined causes a failure, as a vector-matrix product with incompatible dimensions is now computed:

Wolfram Research (2016), NetGraph, Wolfram Language function, https://reference.wolfram.com/language/ref/NetGraph.html (updated 2022).

Text

Wolfram Research (2016), NetGraph, Wolfram Language function, https://reference.wolfram.com/language/ref/NetGraph.html (updated 2022).

CMS

Wolfram Language. 2016. "NetGraph." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/NetGraph.html.

APA

Wolfram Language. (2016). NetGraph. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NetGraph.html

BibTeX

@misc{reference.wolfram_2024_netgraph, author="Wolfram Research", title="{NetGraph}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/NetGraph.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_netgraph, organization={Wolfram Research}, title={NetGraph}, year={2022}, url={https://reference.wolfram.com/language/ref/NetGraph.html}, note=[Accessed: 17-November-2024 ]}