ClassifierMeasurements

ClassifierMeasurements[classifier,testset,prop]

gives measurements associated with property prop when classifier is evaluated on testset.

ClassifierMeasurements[classifier,testset]

yields a measurement report that can be applied to any property.

ClassifierMeasurements[data,…]

uses classifications data instead of a classifier.

ClassifierMeasurements[…,{prop1,prop2,…}]

gives properties prop1, prop2, etc.

Details and Options

  • Measurements are used to determine the performance of a classifier on data that was not used for training purposes (the test set).
  • Possible measurements include classification metrics (accuracy, likelihood, etc.), visualizations (confusion matrix, ROC curve, etc.) or specific examples (such as the worst classified examples).
  • Classifiers can be a ClassifierFunction or a neural net (NetGraph, NetChain, etc.) that has a "Class" decoder.
  • In ClassifierMeasurements[data,…], the classifications data can have the following forms:
  • {class1,class2,…}classifications from a classifier (human, algorithm, etc.)
    {dist1,dist2,…}class distributions obtained by a classifier
    {<|class1p1,…|>,<|class1q1,…|>,…}classification probabilities obtained by a classifier
  • ClassifierMeasurements[…,opts] specifies that the classifier should use the options opts when applied to the test set. Possible options are as given in ClassifierFunction.
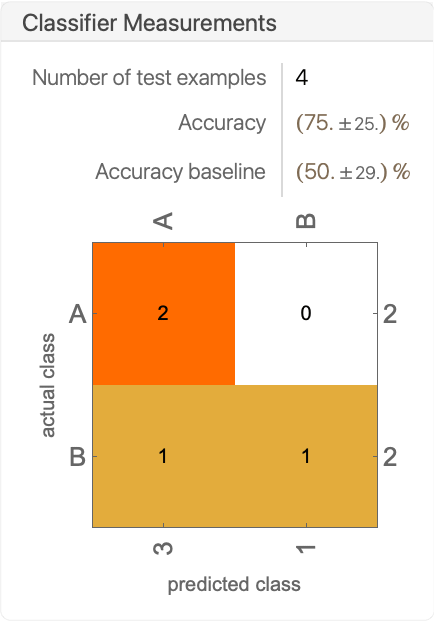
  • ClassifierMeasurements[classifier,testset] returns a ClassifierMeasurementsObject[…] that displays as a report panel, such as:
  • ClassifierMeasurementsObject[…][prop] can be used to obtain the property prop. When repeated property lookups are required, this is typically more efficient than using ClassifierMeasurements every time.
  • ClassifierMeasurementsObject[…][prop,opts] specifies that the classifier should use the options opts when applied to the test set. These options supersede original options given to ClassifierMeasurements.
  • ClassifierMeasurements has the same options as ClassifierFunction[…], with the following additions:
  • Weights Automaticweights to be associated with test set examples
    ComputeUncertainty Falsewhether measures should be given with their statistical uncertainty
  • When ComputeUncertaintyTrue, numerical measures will be returned as Around[result,err] where err represents the standard error (corresponding to a 68% confidence interval) associated with measure result.
  • Possible settings for Weights include:
  • Automaticassociates weight 1 with all test examples
    {w1,w2,…}associates weight wi with the i^(th) test examples
  • Changing the weight of a test example from 1 to 2 is equivalent to duplicating the example.
  • Weights affect measures as well as their uncertainties.
  • Properties returning a single numeric value related to classification abilities on the test set include:
  • "Accuracy"fraction of correctly classified examples
    "Accuracy"ntop-n accuracy
    "AccuracyBaseline"accuracy if predicting the commonest class
    "CohenKappa"Cohen's kappa coefficient
    "Error"fraction of incorrectly classified examples
    "GeometricMeanProbability"geometric mean of the actual-class probabilities
    "LogLikelihood"log-likelihood of the model given the test set
    "MeanCrossEntropy"mean cross entropy over test examples
    "MeanDecisionUtility"mean utility over test example
    "Perplexity"exponential of the mean cross entropy
    "RejectionRate"fraction of examples classified as Indeterminate
    "ScottPi"Scott's pi coefficient
  • Examples classified as Indeterminate are discarded when measuring properties related to classification abilities on the test set, such as "Accuracy", "Error", or "MeanCrossEntropy".
  • Confusion matrix–related properties include:
  • "ConfusionMatrix"counts cij of class i examples classified as class j
    "ConfusionMatrixPlot"plot of the confusion matrix
    "ConfusionMatrixPlot"{c1,c2,…}confusion matrix plot restricted to classes c1, c2, etc.
    "ConfusionMatrixPlot"nconfusion matrix plot for the worst n-class subset
    "ConfusionFunction"function giving confusion matrix values
    "TopConfusions"pairs of classes that are most confused
    "TopConfusions"nn most confused class pairs
  • Timing-related properties include:
  • "EvaluationTime"time needed to classify one example of the test set
    "BatchEvaluationTime"marginal time to classify one example in a batch
  • Properties returning one value for each test-set example include:
  • "DecisionUtilities"value of the utility function for each example
    "Probabilities"actual-class classification probabilities for each example
    "SHAPValues"Shapley additive feature explanations for each example
  • "SHAPValues" assesses the contribution of features by comparing predictions with different sets of features removed and then synthesized. The option MissingValueSynthesis can be used to specify how the missing features are synthesized. SHAP explanations are given as odds ratio multipliers with respect to the class training prior. "SHAPValues"n can be used to control the number of samples used for the numeric estimations of SHAP explanations.
  • Properties related to probability calibration include:
  • "CalibrationCurve"probability calibration curve in logit scale
    "LinearCalibrationCurve"probability calibration curve in linear scale
    "CalibrationData"probability calibration curve data
  • Properties returning graphics include:
  • "AccuracyRejectionPlot"plot of the accuracy as function of the rejection rate
    "ICEPlots"Individual Conditional Expectation (ICE) plots
    "ProbabilityHistogram"histogram of actual-class probabilities
    "Report"panel reporting main measurements
    "ROCCurve"Receiver Operating Characteristics curve for each class
    "SHAPPlots"Shapley additive feature explanations plot for each class
  • Properties returning examples from the test set include:
  • "Examples"all test examples
    "Examples"{i,j}all class i examples classified as class j
    "BestClassifiedExamples"examples having the highest actual-class probability
    "WorstClassifiedExamples"examples having the lowest actual-class probability
    "CorrectlyClassifiedExamples"examples correctly classified
    "MisclassifiedExamples"examples misclassified
    "TruePositiveExamples"true positive test examples for each class
    "FalsePositiveExamples"false positive test examples for each class
    "TrueNegativeExamples"true negative test examples for each class
    "FalseNegativeExamples"false negative test examples for each class
    "IndeterminateExamples"test examples classified as Indeterminate
    "LeastCertainExamples"examples having the highest distribution entropy
    "MostCertainExamples"examples having the lowest distribution entropy
  • Examples are given in the form inputiclassi, where classi is the actual class from the test set.
  • Properties such as "WorstClassifiedExamples" or "MostCertainExamples" output up to 10 examples. ClassifierMeasurementsObject[…][propn] can be used to output n examples.
  • Properties returning one measure for each class include:
  • "AreaUnderROCCurve"area under the ROC curve for each class
    "ClassMeanCrossEntropy"mean cross entropy for each class
    "ClassRejectionRate"rejection rate for each class
    "F1Score"F1 score for each class
    "FalseDiscoveryRate"false discovery rate for each class
    "FalseNegativeRate"false negative rate for each class
    "FalsePositiveRate"false positive rate for each class
    "MatthewsCorrelationCoefficient"Matthews correlation coefficient for each class
    "NegativePredictiveValue"negative predictive value for each class
    "Precision"precision of classification for each class
    "Recall"recall rate of classification for each class
    "Specificity"specificity for each class
    "TruePositiveNumber"number of true positive examples
    "FalsePositiveNumber"number of false positive examples
    "TrueNegativeNumber"number of true negative examples
    "FalseNegativeNumber"number of false negative examples
  • ClassifierMeasurementsObject[…][propclass] can be used to only return the measure associated with the specified class.
  • ClassifierMeasurementsObject[…][prop<|class1w1,class2w2,…|>] can be used to return a weighted average of each class measure.
  • ClassifierMeasurementsObject[…][propf] can be used to apply function f to the returned class measures (e.g. ClassifierMeasurementsObject[…][propMean]).
  • Properties such as "Precision" or "Recall" give one measure for each possible "positive class". The "negative class" is the union of all the classes that are not the positive class. For such properties, one can average the measures for all possible positive classes using ClassifierMeasurementsObject[…][propaverage], where average can be:
  • "MacroAverage"takes the mean of the measures
    "WeightedMacroAverage"weights each measure by its related class frequency
    "MicroAverage"joins true positive/true negative etc. examples of all classes to give a unique measure
  • Other properties include:
  • "ClassifierFunction"ClassifierFunction[…] being measured
    "Properties"list of measurement properties available

Examples

open allclose all

Basic Examples  (4)

Train a classifier on a training set:

Define a test set:

Measure the accuracy of the classifier on the test set:

Visualize the confusion matrix:

Measure several properties at once:

Train a classifier on a training set:

Generate a measurement object of the classifier on a test set:

Obtain the list of measurement properties available:

Obtain the accuracy from the measurement object:

Obtain the accuracy along with its statistical uncertainty due to finite test-set size:

Obtain several measures:

Measure the accuracy directly from classified examples:

Obtain a measurement report:

Measure the mean cross entropy from classification probabilities:

Measure the mean cross entropy from class distributions:

Define a neural net classifier:

Train the neural net on a training set:

Measure the accuracy of this classifier net on a test set:

Visualize the confusion matrix:

Scope  (7)

Decision Metrics  (3)

Measure the accuracy of classified examples against their true labels:

Obtain the statistical uncertainty on this measure:

Compare the accuracy to a baseline (always predicting the most likely test-set class, "B" in this case):

Measure the error on the same data:

Check that error and accuracy sum to 1:

Measure the accuracy using a higher weight for the last two examples:

Create a training set and a test set on MNIST data:

Train a model on the training set:

Compute the accuracy of the model on the test set:

Compute the "top-3" accuracy of the model on the test set (classification is considered correct if the true class is among the three predicted classes with the highest probabilities):

Measure Cohen's kappa coefficient on classified examples against their true labels:

Measure Scott's pi on the same data:

Confusion Matrix & Example Extraction  (1)

Create a training set and a test set on MNIST data:

Train a model on the training set:

Create a classifier measurements object for this classifier on the test set:

Find the 10 test examples that have the worst classification (lowest probabiity for the correct class):

Compute their correct-class probability:

Find the 10 test examples that have the best classification:

Compute their correct-class probability:

Visualize the confusion matrix:

Extract the confusion matrix:

Extract the number of test examples of "3" classified as a "5":

Find the 5 most frequent class confusions:

Restrict the confusion matrix to the set of 3 classes that are the most confused with each other:

Restrict the confusion matrix to the set of 3 classes that are the least confused with each other:

Restrict the confusion matrix to classes "1", "4" and "9":

Extract the examples of "4" that are confused with a "9":

Probabilistic Metrics  (1)

Load the Fisher's Irises dataset:

Create a training set and a test set:

Train a classifier to recognize the iris species from their attributes:

Measure the log-likelihood of the test set (total log-probabilities of correct classes):

Measure the mean cross-entropy:

The mean cross-entropy is the average negative log-likelihood:

Measure the geometric mean of the probabilities for the correct class:

This geometric mean is related to the mean cross-entropy:

Probability Calibration  (1)

Create a training set and a test set on MNIST data:

Train a random forest classifier for which the probability calibration is deactivated:

Visualize the reliability diagram (a.k.a calibration curve) of the classifier on the test set in a logit scale:

Visualize the same reliability diagram using a linear scaling:

Train a classifier where the calibration is activated:

Visualize its reliability diagram in logit scale:

Visualize its reliability diagram in linear scale:

Binary-Classification Metrics  (1)

Load the Fisher's Irises dataset:

Create a training set and a test set:

Train a classifier to recognize the iris species from their attributes:

Compute a ROC curve for each possible "positive" class:

Compute the area under these curves:

Measure the F1 score for each possible "positive" class:

Measure the F1 score if versicolor is the "positive" class:

Take the mean of all F1 scores:

Weight each score according to the class prior:

Compute F1 scores by joining true positive/true negative, etc. examples of all classes to give a unique measure:

Options  (6)

ClassPriors  (1)

Load the training set and test set of the "Satellite" dataset:

Train a classifier on the training set:

Train a classifier on the training set:

Visualize the confusion matrix obtained when the classifier has a different value of ClassPriors:

Perform the same operation by first generating a ClassifierMeasurementsObject:

IndeterminateThreshold  (1)

Load the training set and test set of the "Titanic" dataset:

Train a classifier on the training set:

Visualize the confusion matrix of the classifier on the test set:

Visualize the confusion matrix obtained when the classifier has a different value of IndeterminateThreshold:

Measure the accuracy of the classifier on the test set for different values of IndeterminateThreshold:

Visualize the accuracy-versus-rejection curve:

TargetDevice  (1)

Train a classifier using a neural network:

Measure the accuracy of the classifier on a test set for different setting of TargetDevice:

UtilityFunction  (1)

Load the training set and test set of the "Mushroom" dataset:

Train a classifier on a part of the training set:

Visualize the confusion matrix of the classifier on the test set:

Visualize the confusion matrix obtained when the classifier has a different value of UtilityFunction:

Perform the same operation by first generating a ClassifierMeasurementsObject:

ComputeUncertainty  (1)

Train a classifier that classifies movie review snippets as "positive" or "negative":

Generate a ClassifierMeasurements[…] object using a test set:

Obtain a measure of the accuracy along with its uncertainty:

Obtain a measure of other properties along with their uncertainties:

Weights  (1)

Create a classifier on a training set:

Generate a measurement object while specifying the weights that each test example has:

Compute the accuracy:

Weights can also be modified when using the measurement object:

Uncertainties are also affected by weights:

Applications  (2)

Train a classifier on the Fisher Iris dataset to predict the species of Iris (setosa, versicolor, virginica) from four measured features:

Measure the accuracy of the classifier on a test set:

Generate a confusion matrix to visualize the actual and predicted classifications of the test set using the classifier:

Extract examples of class "versicolor" being misclassified as "virginica":

Return the confusion matrix as a set of associations:

Train a classifier on a sample of the MNIST dataset:

Generate a ClassifierMeasurementsObject of the classifier on the MNIST test set:

Extract examples of 9 confused with 0:

Extract the 20 worst classified examples:

Compute the F-score of each class to find for which class the classifier should be improved:

Find the minimal value for the rejection threshold in order for the accuracy to be above 95%:

Visualize the confusion matrix and compute the F-scores with this rejection threshold:

Visualize the 3 most confused classes:

Wolfram Research (2014), ClassifierMeasurements, Wolfram Language function, https://reference.wolfram.com/language/ref/ClassifierMeasurements.html (updated 2021).

Text

Wolfram Research (2014), ClassifierMeasurements, Wolfram Language function, https://reference.wolfram.com/language/ref/ClassifierMeasurements.html (updated 2021).

CMS

Wolfram Language. 2014. "ClassifierMeasurements." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/ClassifierMeasurements.html.

APA

Wolfram Language. (2014). ClassifierMeasurements. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ClassifierMeasurements.html

BibTeX

@misc{reference.wolfram_2024_classifiermeasurements, author="Wolfram Research", title="{ClassifierMeasurements}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/ClassifierMeasurements.html}", note=[Accessed: 17-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_classifiermeasurements, organization={Wolfram Research}, title={ClassifierMeasurements}, year={2021}, url={https://reference.wolfram.com/language/ref/ClassifierMeasurements.html}, note=[Accessed: 17-December-2024 ]}