NetMeasurements[net,data,measurement]
computes the requested measurement for the net evaluated on data.
NetMeasurements[net,data,{mspec1,mspec2,…}]
computes a list of measurements for the net evaluated on data.


NetMeasurements
NetMeasurements[net,data,measurement]
computes the requested measurement for the net evaluated on data.
NetMeasurements[net,data,{mspec1,mspec2,…}]
computes a list of measurements for the net evaluated on data.
Details and Options




- NetMeasurements is an extension of ClassifierMeasurements and PredictorMeasurements that offers a few features that make it particularly well suited for neural nets. For example, the measurements are all implemented efficiently in the computational graph of the net and can be calculated on the GPU, which makes NetMeasurements applicable to the large datasets often used when training nets.
- A net can be any NetChain, NetGraph, NetModel or similar construct that could be supplied to NetTrain.
- The data can be in any form accepted by NetTrain, including:
-
{input1output1,input2output2,…} a list of input-output pairs port1{data11,…},port2{…},… data corresponding to each port in the net "dataset" a named dataset from the Wolfram Data Repository - Named datasets that are commonly used as examples for neural net applications include the following:
-
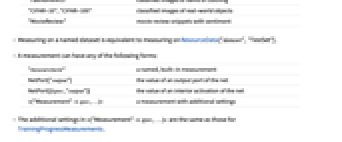
"MNIST" classified handwritten digits "FashionMNIST" classified images of items of clothing "CIFAR-10","CIFAR-100" classified images of real-world objects "MovieReview" movie review snippets with sentiment - Measuring on a named dataset is equivalent to measuring on ResourceData["dataset","TestSet"].
- A measurement can have any of the following forms:
-
"measurement" a named, built-in measurement NetPort["output"] the value of an output port of the net NetPort[{lspec,"output"}] the value of an interior activation of the net <|"Measurement"spec,…|> a measurement with additional settings - The additional settings in <|"Measurement"spec,…|> are the same as those for TrainingProgressMeasurements.
- All properties from Information can be used as built-in measurements.
- For nets that contain CrossEntropyLossLayer, the following built-in measurements are available:
-
"Accuracy" fraction of correctly classified examples "Accuracy"n fraction of examples with the correct result in the top n "AreaUnderROCCurve" area under the ROC curve for each class "CohenKappa" Cohen's kappa coefficient "ConfusionMatrix" counts cij of class i examples classified as class j "ConfusionMatrixPlot" plot of the confusion matrix "Entropy" entropy measured in nats "ErrorRate" fraction of incorrectly classified examples "ErrorRate"n fraction of examples with the incorrect result in the top n "F1Score" F1 score for each class "FScore"β Fβ score for each class "FalseDiscoveryRate" false discovery rate for each class "FalseNegativeNumber" number of false negative examples "FalseNegativeRate" false negative rate for each class "FalseOmissionRate" false omission rate for each class "FalsePositiveNumber" number of false positive examples "FalsePositiveRate" false positive rate for each class "Informedness" informedness for each class "Markedness" markedness for each class "MatthewsCorrelationCoefficient" Matthews correlation coefficient for each class "NegativePredictiveValue" negative predictive value for each class "Perplexity" exponential of the entropy "Precision" precision for each class "Recall" recall rate for each class "ROCCurve" receiver operating characteristics (ROC) curve for each class "ROCCurvePlot" plot of the ROC curve "ScottPi" Scott's pi coefficient "Specificity" specificity for each class "TrueNegativeNumber" number of true negative examples "TruePositiveNumber" number of true positive examples - For nets that contain MeanSquaredLossLayer or MeanAbsoluteLossLayer, the following built-in measurements are available:
-
"FractionVarianceUnexplained" the fraction of output variance left unexplained by the net "IntersectionOverUnion" intersection over union for bounding boxes "MeanDeviation" mean absolute value of the residuals "MeanSquare" mean square of the residuals "RSquared" coeficient of determination 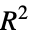
"StandardDeviation" root mean square of the residuals - The following options are supported:
-
BatchSize Automatic how many examples to process in a batch LossFunction Automatic the loss function for assessing outputs NetEvaluationMode "Test" how training-specific layers should behave TargetDevice "CPU" the target device on which to perform measurements WorkingPrecision Automatic precision of floating-point calculations
Examples
open all close allBasic Examples (1)
Scope (2)
Take a number of measurements for a trained LeNet on the MNIST test data. Set up a neural net and test data:
Measure the precision and recall:
Measure the macro-averaged precision and micro-averaged recall:
Measure the mean activation of the logits:
Plot the mean activations of the first convolutional layer's filters:
Get the raw data for the confusion matrix:
Plot the ROC curve for class 1:
Measure the error rate of one of the outputs for a multitask trained network for the CIFAR-100 dataset:
Properties & Relations (2)
NetMeasurements makes use of caching to speed up repeated measurements:
The caching also speeds up similar measurements:
The "IntersectionOverUnion" measurement expects the input and target bounding boxes to be supplied as lists with the form {x1,y1,x2,y2}, where (x1,y1) and (x2,y2) are the coordinates describing the bottom-left and top-right corners of a bounding box.
The calculation of intersection over union is equivalent to the following Mathematica function:
Possible Issues (1)
Trying to measure an output port being used for the LossFunction can fail:
A simple workaround is to create an additional output port to measure and explicitly label the test data:
Tech Notes
Related Guides
History
Text
Wolfram Research (2019), NetMeasurements, Wolfram Language function, https://reference.wolfram.com/language/ref/NetMeasurements.html.
CMS
Wolfram Language. 2019. "NetMeasurements." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NetMeasurements.html.
APA
Wolfram Language. (2019). NetMeasurements. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NetMeasurements.html
BibTeX
@misc{reference.wolfram_2025_netmeasurements, author="Wolfram Research", title="{NetMeasurements}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/NetMeasurements.html}", note=[Accessed: 03-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_netmeasurements, organization={Wolfram Research}, title={NetMeasurements}, year={2019}, url={https://reference.wolfram.com/language/ref/NetMeasurements.html}, note=[Accessed: 03-March-2026]}