WOLFRAM

Wolfram Language & System Documentation Center

LinearRecurrence[ker,init,n]

gives the sequence of length n obtained by iterating the linear recurrence with kernel ker starting with initial values init.

LinearRecurrence[ker,init,{n}]

gives the n^(th) term.

LinearRecurrence[ker,init,{nmin,nmax}]

yields terms nmin through nmax.

Details
Details and Options Details and Options
Examples  
Basic Examples  
Scope  
Generalizations & Extensions  
Applications  
Properties & Relations  
Possible Issues  
Neat Examples  
See Also
Related Guides
Related Links
History
Cite this Page

LinearRecurrence

LinearRecurrence[ker,init,n]

gives the sequence of length n obtained by iterating the linear recurrence with kernel ker starting with initial values init.

LinearRecurrence[ker,init,{n}]

gives the n^(th) term.

LinearRecurrence[ker,init,{nmin,nmax}]

yields terms nmin through nmax.

Details

  • The ker and init can involve arbitrary symbolic expressions, as well as arrays.
  • The initial list init must be at least as long as the kernel list ker.
  • If init is longer than ker, only the last Length[ker] elements are used.
  • LinearRecurrence[{a1,…,ad},{y1,…,yd},n] iterates the recurrence equation 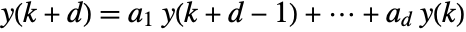with initial conditions , …, .
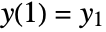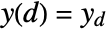  • When coefficients ai and initial values yj are arrays, then the iterated recurrence is interpreted as 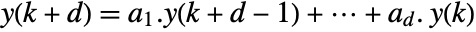with dot products of values and the reversed coefficients.
  • If the initial values yj have dimensions {m1,…,ms} then the coefficients ai must either be scalar or must have dimensions {m1,m1}.

Examples

open all close all

Basic Examples  (3)

Solve an initial-value problem for a first-order difference equation with kernel {-3, 1}:

Find the first few Fibonacci numbers:

Scope  (2)

LinearRecurrence works with symbolic kernels and initial values:

LinearRecurrence works with arrays:

Generalizations & Extensions  (2)

Generate a subset of values from a given range:

Get only the last value from an iteration:

Applications  (2)

Generate recursive sequences, including a Padovan sequence:

Pell numbers:

Pell–Lucas numbers:

Perrin sequence:

Efficiently compute the n^(th) term of a linear recurrence for large n:

Properties & Relations  (1)

RSolve finds a symbolic solution for difference equations:

LinearRecurrence generates a procedural solution:

Obtain the same result using RSolveValue:

Possible Issues  (1)

Initial values are longer than the kernel:

Only the last terms are used:

Neat Examples  (1)

Wolfram Research (2008), LinearRecurrence, Wolfram Language function, https://reference.wolfram.com/language/ref/LinearRecurrence.html (updated 2017).

Text

Wolfram Research (2008), LinearRecurrence, Wolfram Language function, https://reference.wolfram.com/language/ref/LinearRecurrence.html (updated 2017).

CMS

Wolfram Language. 2008. "LinearRecurrence." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/LinearRecurrence.html.

APA

Wolfram Language. (2008). LinearRecurrence. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LinearRecurrence.html

BibTeX

@misc{reference.wolfram_2025_linearrecurrence, author="Wolfram Research", title="{LinearRecurrence}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/LinearRecurrence.html}", note=[Accessed: 31-October-2025]}

BibLaTeX

@online{reference.wolfram_2025_linearrecurrence, organization={Wolfram Research}, title={LinearRecurrence}, year={2017}, url={https://reference.wolfram.com/language/ref/LinearRecurrence.html}, note=[Accessed: 31-October-2025]}