LQOutputRegulatorGains[sspec,wts]
gives the state feedback gains for the system specification sspec that minimizes an output cost function with weights wts.
LQOutputRegulatorGains[…,"prop"]
gives the value of the property "prop".


LQOutputRegulatorGains
LQOutputRegulatorGains[sspec,wts]
gives the state feedback gains for the system specification sspec that minimizes an output cost function with weights wts.
LQOutputRegulatorGains[…,"prop"]
gives the value of the property "prop".
Details and Options





- LQOutputRegulatorGains is also known as linear quadratic output regulator, linear quadratic output controller or optimal controller.
- LQOutputRegulatorGains is typically used to stabilize a system or improve its performance.
- The controller is typically given by a state feedback
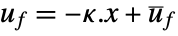 , where
, where 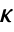 is the computed gain matrix.
is the computed gain matrix. - The inputs u of sys consist of feedback inputs uf and possibly other inputs ue.
- The outputs y of sys consist of regulated outputs yr and possibly other outputs.
- The system specification sspec is the system sys together with the uf and yr specifications.
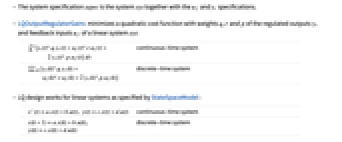
- LQOutputRegulatorGains minimizes a quadratic cost function with weights q, r and p of the regulated outputs yr and feedback inputs uf of a linear system sys:
-
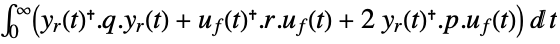
continuous-time system 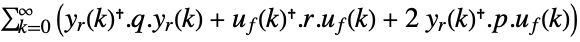
discrete-time system - LQ design works for linear systems as specified by StateSpaceModel:
-
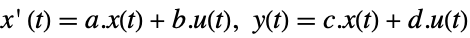
continuous-time system 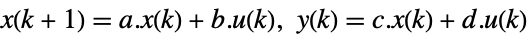
discrete-time system - The resulting feedback gain matrix is then computed as
![kappa=TemplateBox[{{r, _, 1}}, Inverse].x_1 kappa=TemplateBox[{{r, _, 1}}, Inverse].x_1](Files/LQOutputRegulatorGains.en/8.png) :
: -
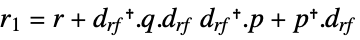
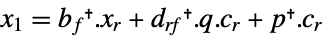
continuous-time system 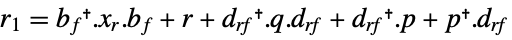
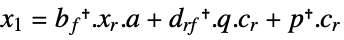
discrete-time system - The matrix xr is the solution of the Riccati equation:
-
![a.x_r+x_r.a-x_1.TemplateBox[{{r, _, 1}}, Inverse].x_1+c_r.q.c_r=0 a.x_r+x_r.a-x_1.TemplateBox[{{r, _, 1}}, Inverse].x_1+c_r.q.c_r=0](Files/LQOutputRegulatorGains.en/13.png)
continuous-time algebraic Riccati equation ![a.x_r.a-x_r-x_1.TemplateBox[{{r, _, 1}}, Inverse].x_1+c_r.q.c_r=0 a.x_r.a-x_r-x_1.TemplateBox[{{r, _, 1}}, Inverse].x_1+c_r.q.c_r=0](Files/LQOutputRegulatorGains.en/14.png)
discrete-time algebraic Riccati equation - The submatrices bf, cr and drf correspond to the feedback inputs uf and regulated outputs yr.
- The weights wts can have the following forms:
-
{q,r} cost function with no cross-coupling {q,r,p} cost function with cross-coupling matrix p - The system specification sspec can have the following forms:
-
StateSpaceModel[…] linear control input and linear state AffineStateSpaceModel[…] linear control input and nonlinear state NonlinearStateSpaceModel[…] nonlinear control input and nonlinear state SystemModel[…] general system model <|…|> detailed system specification given as an Association - The detailed system specification can have the following keys:
-
"InputModel" sys any one of the models "FeedbackInputs" All the feedback inputs uf "RegulatedOutputs" All the regulated outputs yr - The inputs and outputs can have the following forms:
-
{num1,…,numn} numbered inputs or outputs numi used by StateSpaceModel, AffineStateSpaceModel and NonlinearStateSpaceModel {name1,…,namen} named inputs or outputs namei used by SystemModel All uses all inputs or outputs - For nonlinear systems such as AffineStateSpaceModel, NonlinearStateSpaceModel and SystemModel, the system will be linearized around its stored operating point.
- LQOutputRegulatorGains[…,"Data"] returns a SystemsModelControllerData object cd that can be used to extract additional properties using the form cd["prop"].
- LQOutputRegulatorGains[…,"prop"] can be used to directly give the value of cd["prop"].
- Possible values for properties "prop" include:
-
"ClosedLoopPoles" poles of the linearized "ClosedLoopSystem" "ClosedLoopSystem" system csys with ue and 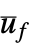 as input and y as output
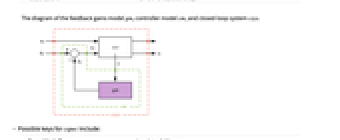
as input and y as output{"ClosedLoopSystem", cspec} detailed control over the form of the closed-loop system "ControllerModel" model cm with 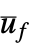 and x as input and uf as output
and x as input and uf as output "Design" type of controller design "DesignModel" model used for the design "FeedbackGains" gain matrix κ or its equivalent "FeedbackGainsModel" model gm with x as input and 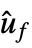 as output
as output"FeedbackInputs" inputs uf of sys used for feedback "InputModel" input model sys "InputCount" number of inputs u of sys "OpenLoopPoles" poles of "DesignModel" "OutputCount" number of outputs y of sys "RegulatedOutputs" outputs yr of sys that are regulated "SamplingPeriod" sampling period of sys "StateCount" number of states x of sys - Possible keys for cspec include:
-
"InputModel" input model in csys "Merge" whether to merge csys "ModelName" name of csys
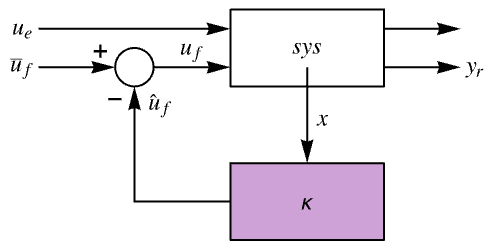
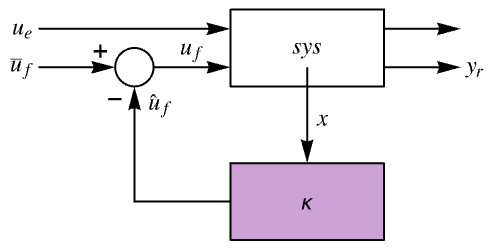
The diagram of the feedback gains model gm, controller model cm, and closed-loop system csys.
Examples
open all close allBasic Examples (2)
Scope (27)
Basic Uses (8)
Compute the state feedback gain of a system with equal weighting for the output and input:
Compute the gain for an unstable system:
The gain stabilizes the unstable system:
Compute the state feedback gains for a multiple-output system:
The dimensions of the result correspond to the number of inputs and the system's order:
Compute the gains for a system with 3 outputs and 2 inputs:
Reverse the weights of the feedback inputs:
Typically, the feedback input with the bigger weight has the smaller norm:
Compute the gains when the cost function contains cross-coupling of the outputs and feedback inputs:
Choose the feedback outputs for multiple-output systems:
Choose the feedback inputs for multiple-input systems:
Compute the gains for a nonlinear system:
The controller is returned as a vector and takes operating points into consideration:
Plant Models (6)
Properties (10)
LQOutputRegulatorGains returns the feedback gains by default:
In general, the feedback is affine in the states:
It is of the form κ0+κ1.x, where κ0 and κ1 are constants:
The systems model of the feedback gains:
An affine systems model of the feedback gains:
The poles of the linearized closed-loop system:
The model used to compute the feedback gains:
The gains of the design model and input model:
Properties related to the input model:
Get the controller data object:
Closed-Loop System (3)
Assemble the closed-loop system for a nonlinear plant model:
The closed-loop system with a linearized model:
Compare the response of the two systems:
Assemble the merged closed-loop of a plant with one disturbance and one feedback input:
The unmerged closed-loop system:
When merged, it gives the same result as before:
Explicitly specify the merged closed-loop system:
Create a closed-loop system with a desired name:
The closed-loop system has the specified name:
The name can be directly used to specify the closed-loop model in other functions:
Applications (2)
Properties & Relations (3)
Equivalent output regulator gains can be computed using LQRegulatorGains:
LQOutputRegulatorGains gives the same result:
Compute the LQ output regulator gains by solving the underlying Riccati equation:
LQOutputRegulatorGains gives the same result:
Compute the gains for a discrete-time system using DiscreteRiccatiSolve:
LQOutputRegulatorGains gives the same result:
Related Guides
History
Introduced in 2010 (8.0) | Updated in 2012 (9.0) ▪ 2014 (10.0) ▪ 2021 (12.3)
Text
Wolfram Research (2010), LQOutputRegulatorGains, Wolfram Language function, https://reference.wolfram.com/language/ref/LQOutputRegulatorGains.html (updated 2021).
CMS
Wolfram Language. 2010. "LQOutputRegulatorGains." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/LQOutputRegulatorGains.html.
APA
Wolfram Language. (2010). LQOutputRegulatorGains. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LQOutputRegulatorGains.html
BibTeX
@misc{reference.wolfram_2025_lqoutputregulatorgains, author="Wolfram Research", title="{LQOutputRegulatorGains}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/LQOutputRegulatorGains.html}", note=[Accessed: 05-September-2025]}
BibLaTeX
@online{reference.wolfram_2025_lqoutputregulatorgains, organization={Wolfram Research}, title={LQOutputRegulatorGains}, year={2021}, url={https://reference.wolfram.com/language/ref/LQOutputRegulatorGains.html}, note=[Accessed: 05-September-2025]}