LandauDistribution
LandauDistribution[μ,σ]
represents a Landau distribution with location parameter μ and scale parameter σ.
represents a Landau distribution with location parameter 0 and scale parameter 1.
Details
- The probability density for value
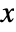 in a Landau distribution is proportional to
in a Landau distribution is proportional to 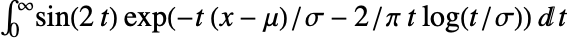 .
. - LandauDistribution allows μ to be any real number and σ any positive real number.
- LandauDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- LandauDistribution[μ,σ] represents a statistical distribution defined and supported on the set
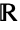 of real numbers and parametrized by a real number μ (called a "location parameter") and by a real number σ (called a "scale parameter"). Overall, the probability density function (PDF) of a Landau distribution is unimodal with a single "peak" (i.e. a global maximum), though its overall shape (its height, its spread, and its concentration near the
of real numbers and parametrized by a real number μ (called a "location parameter") and by a real number σ (called a "scale parameter"). Overall, the probability density function (PDF) of a Landau distribution is unimodal with a single "peak" (i.e. a global maximum), though its overall shape (its height, its spread, and its concentration near the  axis) is determined by the values of μ and σ. In addition, the tails of the PDF are "fat" in the sense that the PDF decreases algebraically rather than decreasing exponentially for large values of
axis) is determined by the values of μ and σ. In addition, the tails of the PDF are "fat" in the sense that the PDF decreases algebraically rather than decreasing exponentially for large values of 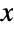 . (This behavior can be observed in the "locally linear behavior" of the log-log plot (LogLogPlot) of the PDF for large
. (This behavior can be observed in the "locally linear behavior" of the log-log plot (LogLogPlot) of the PDF for large 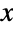 .) The zero-argument form LandauDistribution[] (which is equivalent to LandauDistribution[0,1]) is sometimes referred to as the standard Landau distribution.
.) The zero-argument form LandauDistribution[] (which is equivalent to LandauDistribution[0,1]) is sometimes referred to as the standard Landau distribution. - The Landau distribution was developed by Soviet physicist Lev Landau in a paper published in 1944 as a generalized distribution suitable for describing the energy loss experienced by a "fast" particle (i.e. a particle possessing energies large enough for ionization theory to be applied) as it transverses a layer of matter of fixed (yet small) thickness. As such, the Landau distribution models a number of phenomena across various subfields of physics and chemistry.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Landau distribution. Distributed[x,LandauDistribution[μ,σ]], written more concisely as xLandauDistribution[μ,σ], can be used to assert that a random variable x is distributed according to a Landau distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions for Landau distributions may be given using PDF[LandauDistribution[μ,σ],x] and CDF[LandauDistribution[μ,σ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively, though because of its long tails, the
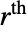 raw and central moments (including the mean and variance) of LandauDistribution are all Indeterminate for
raw and central moments (including the mean and variance) of LandauDistribution are all Indeterminate for 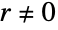 .
. - DistributionFitTest can be used to test if a given dataset is consistent with a Landau distribution, EstimatedDistribution to estimate a Landau parametric distribution from given data, and FindDistributionParameters to fit data to a Landau distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Landau distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Landau distribution.
- TransformedDistribution can be used to represent a transformed Landau distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Landau distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Landau distributions.
- LandauDistribution is closely related to a number of other distributions. For example, LandauDistribution is a specific case of a type-1 StableDistribution in the sense that the PDF of LandauDistribution[μ,σ] is precisely the same as StableDistribution[1,1,1,μ,σ]. Because of this, LandauDistribution is also qualitatively related to several distributions, including CauchyDistribution, LevyDistribution, and NormalDistribution.
Examples
open allclose allBasic Examples (3)
Scope (4)
Applications (2)
Charged particles are bombarding a very thin target. The energy loss spectrum is then described by LandauDistribution. Define Landau function ![]() :
:
Find the maximum of the Landau function:
Find the half-width of the Landau function:
For large arguments, the Landau function behaves as ![]() :
:
Lindhard's first-order approximations to the Landau function:
Properties & Relations (4)
Landau distribution is closed under affine transformations:
Relationships to other distributions:
Landau distribution is a StableDistribution:
Evaluate the density of LandauDistribution using its defining integral representation:
Text
Wolfram Research (2010), LandauDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/LandauDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "LandauDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/LandauDistribution.html.
APA
Wolfram Language. (2010). LandauDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LandauDistribution.html