NMinValue

NMinValue[f,x]

gives the global minimum value of f with respect to x.

NMinValue[f,{x,y,…}]

gives the global minimum value of f with respect to x, y, ….

NMinValue[{f,cons},{x,y,…}]

gives the global minimum value of f subject to the constraints cons.

NMinValue[…,x∈reg]

constrains x to be in the region reg.

Details and Options

NMinValue is also known as global optimization (GO).
NMinValue always attempts to find a global minimum of f subject to the constraints given.
NMinValue is typically used to find the smallest possible values given constraints. In different areas, this may be called the best strategy, best fit, best configuration and so on.

If f and cons are linear or convex, the result given by NMinValue will be the global minimum, over both real and integer values; otherwise, the result may sometimes only be a local minimum.
If NMinValue determines that the constraints cannot be satisfied, it returns Infinity.
NMinValue supports a modeling language where the objective function f and constraints cons are given in terms of expressions depending on scalar or vector variables. f and cons are typically parsed into very efficient forms, but as long as f and the terms in cons give numerical values for numerical values of the variables, NMinValue can often find a solution.
The constraints cons can be any logical combination of:

	lhs==rhs	equations
	lhs>rhs, lhs≥rhs, lhs<rhs, lhs≤rhs	inequalities (LessEqual, …)
	lhsrhs, lhsrhs, lhsrhs, lhsrhs	vector inequalities (VectorLessEqual, …)
	{x,y,…}∈rdom	region or domain specification

NMinValue[{f,cons},x∈rdom] is effectively equivalent to NMinValue[{f,cons&&x∈rdom},x].
For x∈rdom, the different coordinates can be referred to using Indexed[x,i].
Possible domains rdom include:

	Reals	real scalar variable
	Integers	integer scalar variable
	Vectors[n,dom]	vector variable in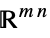
	Matrices[{m,n},dom]	matrix variable in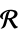
	ℛ	vector variable restricted to the geometric region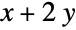

By default, all variables are assumed to be real.
The following options can be given:

AccuracyGoal	Automatic	number of digits of final accuracy sought
EvaluationMonitor	None	expression to evaluate whenever f is evaluated
MaxIterations	Automatic	maximum number of iterations to use
Method	Automatic	method to use
PrecisionGoal	Automatic	number of digits of final precision sought
StepMonitor	None	expression to evaluate whenever a step is taken
WorkingPrecision	MachinePrecision	the precision used in internal computations

The settings for AccuracyGoal and PrecisionGoal specify the number of digits to seek in both the value of the position of the minimum, and the value of the function at the minimum.
NMinValue continues until either of the goals specified by AccuracyGoal or PrecisionGoal is achieved.
The methods for NMinValue fall into two classes. The first class of guaranteed methods uses properties of the problem so that, when the method converges, the minimum found is guaranteed to be global. The second class of heuristic methods uses methods that may include multiple local searches, commonly adjusted by some stochasticity, to home in on a global minimum. These methods often do find the global minimum, but are not guaranteed to do so.
Methods that are guaranteed to give a global minimum when they converge to a solution include:

	"Convex"	use only convex methods
	"MOSEK"	use the commercial MOSEK library for convex problems
	"Gurobi"	use the commercial Gurobi library for convex problems
	"Xpress"	use the commercial Xpress library for convex problems

Heuristic methods include:

	"NelderMead"	simplex method of Nelder and Mead
	"DifferentialEvolution"	use differential evolution
	"SimulatedAnnealing"	use simulated annealing
	"RandomSearch"	use the best local minimum found from multiple random starting points
	"Couenne"	use the Couenne library for non-convex mixed-integer nonlinear problems

Examples

open allclose all

Basic Examples (4)

Find the global minimum value of a univariate function:

Find the global minimum value of a multivariate function:

Find the global minimum value of a function subject to constraints:

Find the global minimum value of a function over a geometric region:

Scope (40)

Basic Uses (12)

Find the minimum value of subject to constraints :

Several linear inequality constraints can be expressed with VectorGreaterEqual:

Use v>= or \[VectorGreaterEqual] to enter the vector inequality sign :

An equivalent form using scalar inequalities:

Use a vector variable :

The inequality may not be the same as due to possible threading in :

To avoid unintended threading in , use Inactive[Plus]:

Use constant parameter equations to avoid unintended threading in :

VectorGreaterEqual represents a conic inequality with respect to the "NonNegativeCone":

To explicitly specify the dimension of the cone, use {"NonNegativeCone",n}:

Find the minimum value:

Find the minimum value of subject to the constraint :

Specify the constraint using a conic inequality with "NormCone":

Find the minimum value:

Find the minimum value of the function subject to the constraint :

Use Indexed to access components of a vector variable, e.g. :

Use Vectors[n,dom] to specify the dimension and domain of a vector variable when it is ambiguous:

Specify non-negative constraints using NonNegativeReals ():

An equivalent form using vector inequality :

Specify non-positive constraints using NonPositiveReals ():

An equivalent form using vector inequalities:

Or constraints can be specified:

Domain Constraints (4)

Specify integer domain constraints using Integers:

Specify integer domain constraints on vector variables using Vectors[n,Integers]:

Specify non-negative integer domain constraints using NonNegativeIntegers ():

Specify non-positive integer domain constraints using NonPositiveIntegers ():

Region Constraints (5)

Find the minimum value of over a region:

Find the minimum distance between two regions:

Find the minimum of such that the triangle and ellipse still intersect:

Find the minimum radius of a disk that contains the given three points:

Using Circumsphere gives the same result directly:

Use to specify that is a vector in with :

Linear Problems (5)

With linear objectives and constraints, when a minimum is found it is global:

The constraints can be equality and inequality constraints:

Use Equal to express several equality constraints at once:

An equivalent form using several scalar equalities:

Use VectorLessEqual to express several LessEqual inequality constraints at once:

Use v<= to enter the vector inequality in a compact form:

An equivalent form using scalar inequalities:

Use Interval to specify bounds on variable:

Convex Problems (7)

Use "NonNegativeCone" to specify linear functions of the form :

Use v>= to enter the vector inequality in a compact form:

Find the minimum value of a convex quadratic function subject to linear constraints:

Find the minimum value of a convex quadratic function subject to a set of convex quadratic constraints:

Find the minimum distance between two convex regions:

Find the minimum value of such that is positive semidefinite:

Minimize convex objective function such that is positive semidefinite and :

Find the minimum value of a convex objective function over a 4-norm unit disk:

Transformable to Convex (4)

Find the minimum perimeter of a rectangle with area 1 such that the height is at most half the width:

This problem is log-convex and is solved by making a transformation {hExp[],wExp[ ]} and taking logarithms to get the convex problem:

Find the minimum value of the quasi-convex function subject to inequality and norm constraints. The objective is quasi-convex because it is a product of a non-negative function and a non-positive function over the domain:

Quasi-convex problems can be solved as parametric convex optimization problems for the parameter :

Plot the objective as a function of the level-set :

For a level-set value between the interval , the smallest objective is found:

The problem becomes infeasible when the level-set value is increased:

Minimize subject to the constraint . The objective is not convex but can be represented by a difference of convex function where and are convex functions:

Plot the region and the minimizing point:

Minimize subject to the constraints . The constraint is not convex but can be represented by a difference of convex constraint where are convex functions:

Plot the region and the minimizing point:

General Problems (3)

Find the minimum value of a linear objective subject to nonlinear constraints:

Find the minimum value of a nonlinear objective subject to linear constraints:

Find the minimum value of a nonlinear objective subject to nonlinear constraints:

Options (7)

AccuracyGoal & PrecisionGoal (2)

This enforces convergence criteria and :

This enforces convergence criteria and , which is not achievable with the default machine-precision computation:

Setting a high WorkingPrecision makes the process convergent:

EvaluationMonitor (1)

Record all the points evaluated during the solution process of a function with a ring of minima:

Plot all the visited points that are close in objective function value to the final solution:

Method (2)

Some methods may give suboptimal results for certain problems:

The automatically chosen method gives the optimal solution for this problem:

Plot the objective function along with the global minimum value:

Use method "NelderMead" for problems with many variables when speed is essential:

StepMonitor (1)

Steps taken by NMinValue in finding the minimum of the classic Rosenbrock function:

WorkingPrecision (1)

With the working precision set to , by default AccuracyGoal and PrecisionGoal are set to :

Applications (6)

Geometry Problems (3)

Find the minimum distance between two disks of radius 1 centered at and . Let be a point on disk 1. Let be a point on disk 2. The objective is to minimize subject to constraints :

Find the radius of a minimal enclosing ball that encompasses a given region:

Find the minimum value of the radius subject to the constraints :

The minimal enclosing ball can be found efficiently using BoundingRegion:

Visualize the enclosing ball:

Find the smallest square that can contain circles of given radius for that do not overlap. Specify the number of circles and the radius of each circle: